一、实操题
1、利用分治思想,给定一个顺序表,编写一个求出其最大值的程序。 根据上述算法思想,补全下列代码。 输入输出示例:当顺序表是 [22,13,34,4,68,15,5,58,36],输出:68
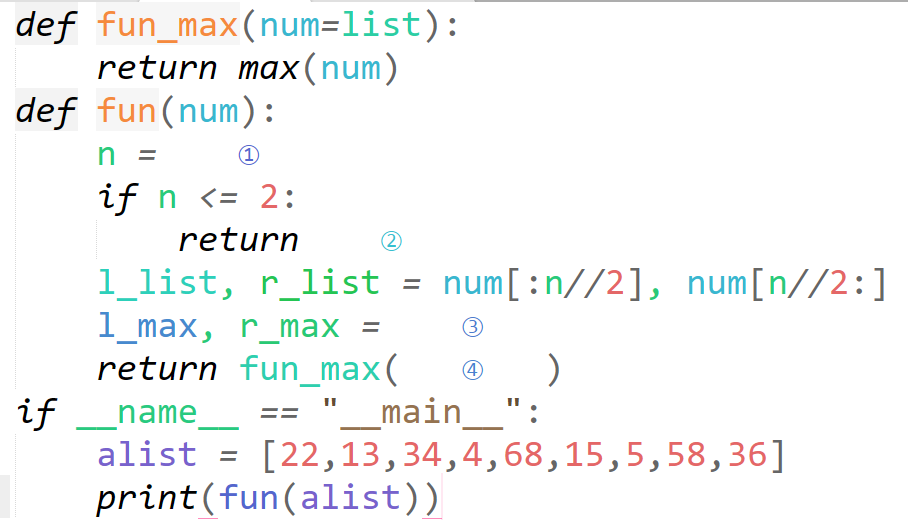
答案解析:① len(num)或等效答案② fun_max(num) 或等效答案③ fun(l_list), fun(r_list) 或等效答案 ④ [l_max, r_max]或等效答案
2、现有n个人依次围成一圈玩游戏,从第1个人开始报数,数到第m个人出局,然后从出局的下一个人开始报数,数到第m个人又出局,...,如此反复到只剩下最后一个是胜利者。设n个人的编号分别为1,2,...,n,打印出局的顺序。 根据上述算法思想,补全下列代码。 输入输出示例:当n=10,m=4,输出如下: 出局的人是: 4 出局的人是: 8 出局的人是: 2 出局的人是: 7 出局的人是: 3 出局的人是: 10 出局的人是: 9 出局的人是: 1 出局的人是: 6 最后胜利者是: 5

答案解析:① range(1,n+1) 或等效答案; ② range(n-1): 或等效答案; ③ (x + k) % len(L) 或等效答案; ④ L[0] 或等效答案;
3、设计一个算法,将一个正整数分解质因数。 程序分析:对n进行分解质因数,应先找到一个最小的质数k,然后按下述步骤完成: (1)如果这个质数恰等于n,则说明分解质因数的过程已经结束,输出即可。 (2)如果n>k,但n能被k整除,则应打印出k的值,并用n除以k的商,作为新的正整数n,重复执行第一步。 (3)如果n不能被k整除,则用k+1作为k的值,重复执行第一步。 根据上述算法思想,补全下列代码。 输入输出示例:当n=105,输出:105= 3*5*7 当n=60,输出:60= 2*2*3*5

答案解析:① range(2,n+1) 或等效答案; ② n%i==0 或等效答案; ③ n=n//i 或等效答案; ④ print(n) 或等效答案;
喵呜刷题:让学习像火箭一样快速,快来微信扫码,体验免费刷题服务,开启你的学习加速器!








