一、单选题
1、
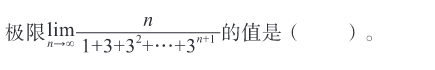
A 0
B
C 1
D 2
答案解析:

2、
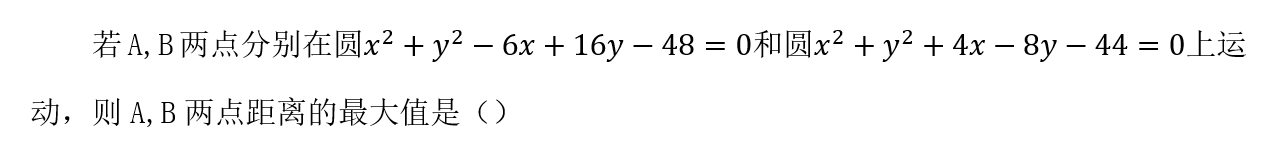
A 13
B 32
C 36
D 38
答案解析:

3、3.
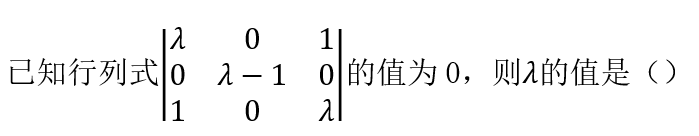
A -1或1
B -1或2
C -1或-2
D 0或2
答案解析:
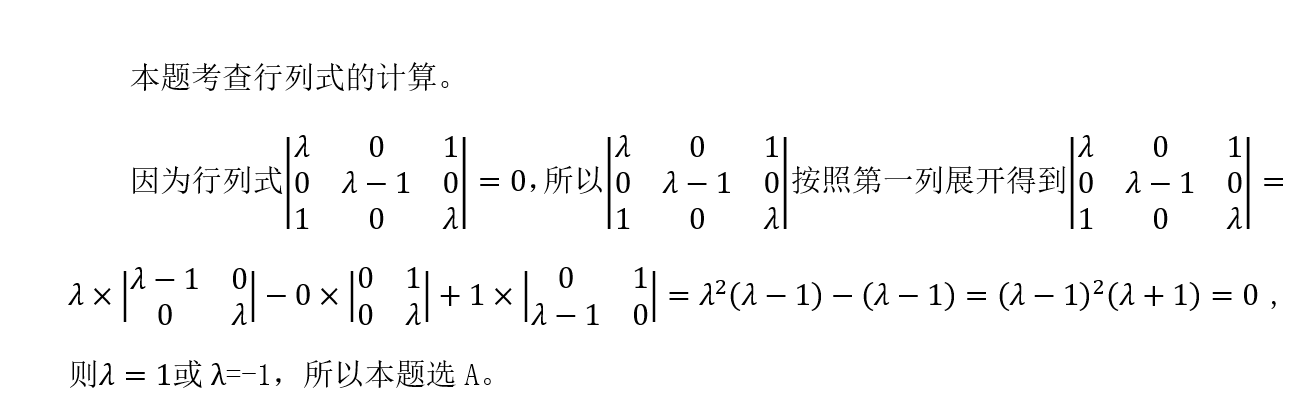
4、
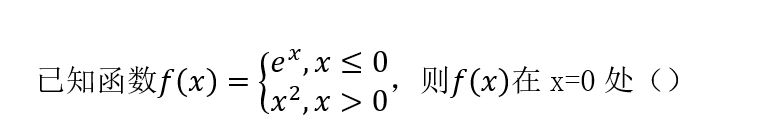
A 连续
B 左连续但不右连续
C 右连续但不左连续
D 既不左连续也不右连续
答案解析:
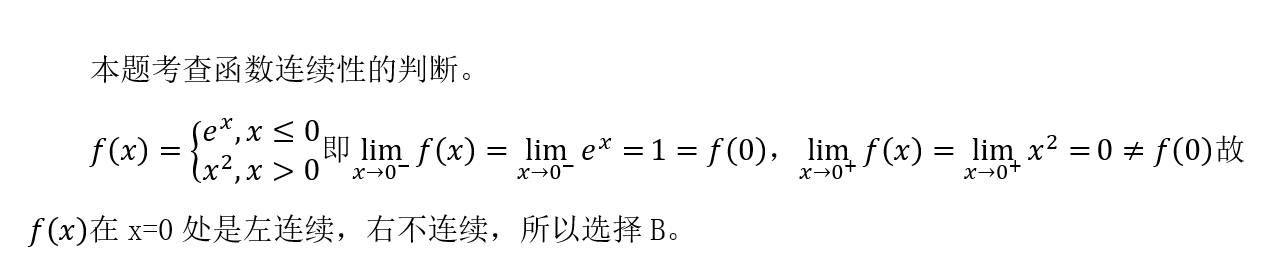
5、5.

A 2
B 6
C 12
D 18
答案解析:
6、

A
B
C
D
答案解析:

7、南宋时期数学家秦九韶在数学上的主要成就是()
A 二分法
B 碾转相除法
C 大衍求一术
D 勾股定理
答案解析:
本题考查数学史的相关知识。
秦九韶于1247年完成数学名著《数书九章》,并创造了“大衍求一术”。这不仅在当时处于世界领先地位,在近代数学和现代电子计算设计中,也起到了重要作用,被称为“中国剩余定理”。
8、下列不能用尺规(无刻度的直尺和圆规)作图的是()
A 过一点做已知直线的垂线
B 已知底边和底边上的高作等腰三角形
C 已知斜边和直角边作直角三角形
D 作任意角的三等分线
答案解析:
本题考查尺规作图的内容。
不可能用尺规作图完成的作图题包括三等分角即三等分一个任意角;倍立方问题即作一个立方体使它的体积是已知立方体的两倍;化圆为方即作一个正方形使它的面积等于已知圆的面积。故本题选D。
二、简答题
9、
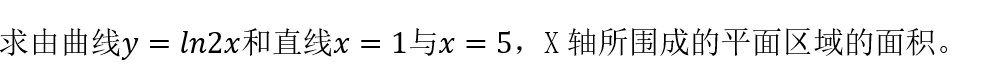
正确答案:
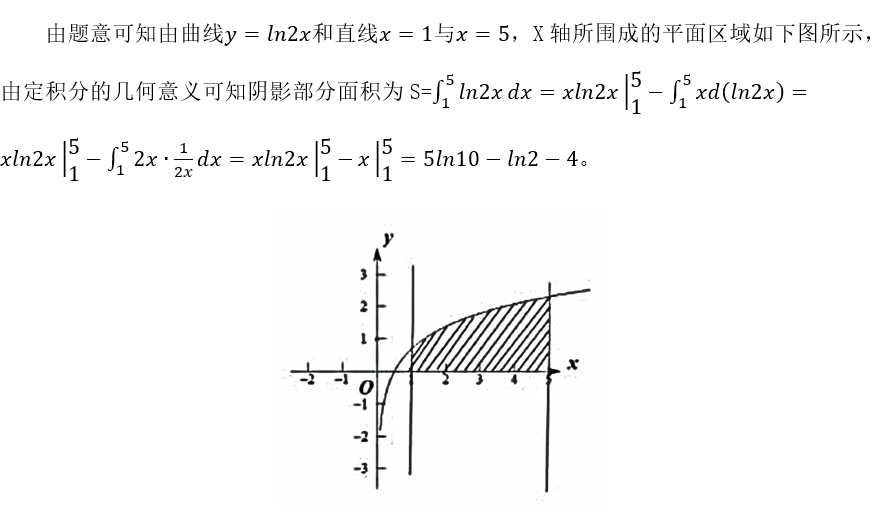
答案解析:
本题考查了定积分求平面面积。
10、已知动点P与定点A(0,0,1)的距离等于点P到直线z=4距离的一半。(1)求动点P的轨迹方程。(2)动点P的轨迹方程所表示的几何图形是什么?
正确答案:

答案解析:
本题考查立体几何的相关知识。
11、不透明的袋子中有10个完全相同的乒乓球,分别标有数字1到10,从袋中随机摸出1个球记录标号后放回袋中,再随机摸出1个球,记录标号后也放回袋中。(1)求两次摸球的标号之和是3的概率;(2)求两次摸球的标号最大是7的概率。
正确答案:

答案解析:
本题考查统计与概率的相关知识。
12、列举义务教育阶段一元二次方程的三种不同解法。
正确答案:

答案解析:
本题考查的是初中学科知识一元二次方程的求解方法。
13、简述义务教育阶段统计内容中数据分析的主要过程,给出描述数据集中趋势和离散程度的统计量(各写出2个)。
正确答案:
(1)数据分析的主要过程包括收集数据,整理数据,描述数据,分析数据,得出结论。学生可以通过全面调查或抽样调查收集数据,然后用划记法记录数据,列成表格,再选用合适的统计图来描述数据,比如可以选用条形图,扇形图,折线图或直方图。最后分析数据,研究数据的平均数,中位数,方差等来得出一些结论。
(2)描述数据的集中趋势的统计量:平均数和中位数;描述数据的波动程度的统计量:方差和标准差。
答案解析:
本题考查统计与概率的相关知识。
三、解答题
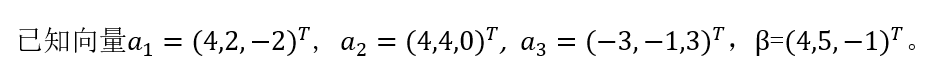
14、
正确答案:
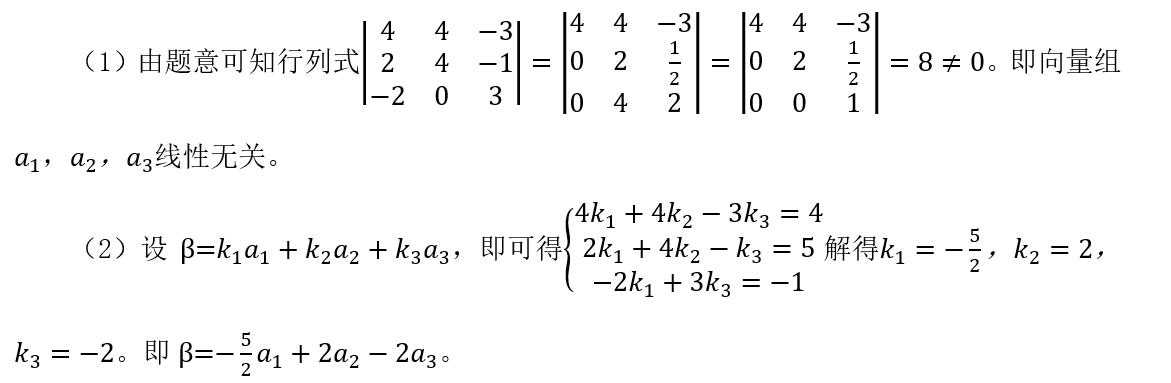
答案解析:
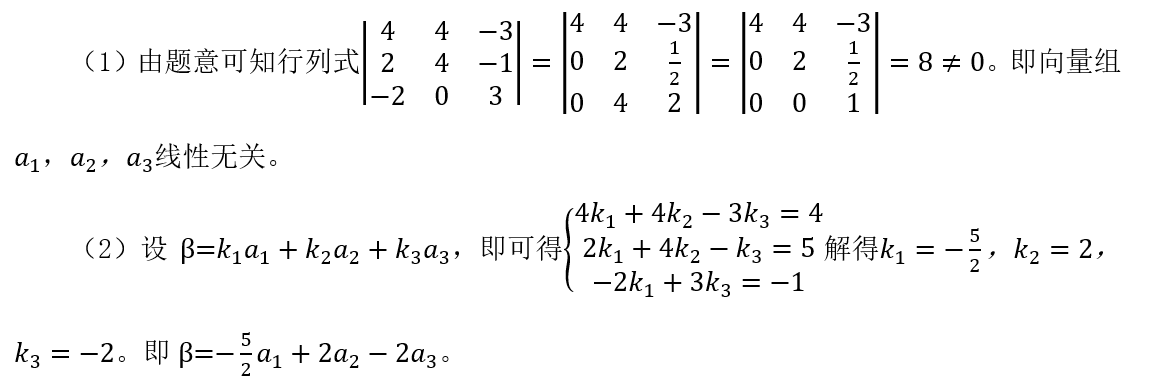
四、简答题
15、写出义务教育阶段一元一次不等式的性质(2条即可);一元一次不等式的性质与解一元一次不等式的关系,并举例说明。
正确答案:

答案解析:
本题考查一元一次不等式的性质和求解。
五、案例分析题
 。
。
16、(1)给出该例题的求解方法;(2)指出该教师对学生的引导有哪些合理和不足之处。
正确答案:

答案解析:
本题考查数学学科知识、课程标准、教学知识。
六、教学设计题
 。
。
17、根据上述片段,完成下列任务:(1)写出其中蕴含的主要数学思想方法。(6分)(2)完成“绝对值”这节课的教学设计,要求写出教学目标、教学重难点和主要教学过程(含情境导入、概念理解、概念巩固)。(24分)
正确答案:
(1)分类与整合的数学思想方法。
(2)教学目标:
知识与技能目标:能够理解绝对值的概念,能求出一个有理数的绝对值。
过程与方法目标:经历用数学符号表达绝对值的过程,发展抽象思维,通过对正数、负数及零的绝对值的讨论,提升分类讨论的能力。
情感态度与价值观目标:体会数学与人类生活的密切联系,在学习过程中获得成就感。
教学重点:掌握绝对值的概念。
教学难点:从绝对值的几何定义中理解它的代数解释。
教学过程:
情境导入环节:
教师创设情境:两辆汽车分别从同一处出发,分别向东、西方向行驶10千米,教师提出问题:它们行驶的路程相等吗?如何区分他们的运动呢?启发学生思考,从而引出课题。
新课讲授环节:


答案解析:
本题考查教学设计。
喵呜刷题:让学习像火箭一样快速,快来微信扫码,体验免费刷题服务,开启你的学习加速器!








