一、单选题
1、

A 0
B 1
C
D
答案解析:

本题考查两个基本公式。
2、下列命题中正确的是( )
A 若n阶行列式D=0,那么D中有两行元素相同
B 若n阶行列式D=0,那么D中有两行元素对应成比例
C 若三阶行列式D中有6个元素为零,则D=0
D 若三阶行列式D中有7个元素为零,则D=0
答案解析:

3、

A 平行
B 直线在平面内
C 垂直
D 相交但不垂直
答案解析:

4、

A
B
C
D
答案解析:
本题考查函数在某点连续的定义,根据函数在某点处连续的定义可知,选A。
5、

A -2
B 2
C
D
答案解析:

6、

A
B
C
D
答案解析:
本题考查离散型随机变量的方差,由离散型随机变量的方差公式可知,选B。
7、数学发展史上曾经历过三次危机,触发第三次数学危机的事件是( )
A 无理数的发现
B 微积分创立
C 罗素悖论
D 数学命题的机器证明
答案解析:
本题考查数学史
8、在某次测试中,用所有参加测试学生某题的平均分除以该题分值,得到的结果是( )
A 区分度
B 难度
C 信度
D 效度
答案解析:
本题考查数学测验的统计指标
二、简答题
9、

正确答案:


答案解析:
本题考查线性变换。
10、

正确答案:

答案解析:
本题考查齐次线性方程组解的求法。
11、王强是一位快递员,他负责由A到B地的送货任务,送货方式为开汽车或者电动车,他分别记录了开汽车和骑电动车各100次所用的送货时间,经过数据分析得到如下数据:开汽车:平均用时24分钟,方差为36;骑电动车:平均用时34分钟,方差为4。(1)根据上述数据,你会建议王强选择哪种送货方式?请说明理由。(3分)(2)分别用X和Y表示开汽车和骑电动车所用的时间,X和Y的分布密度曲线如图所示。(假设这些曲线具有轴对称性,为达到准时送达的目的,如果某次送货有38分钟可用,应该选择哪种送货方式?如果某次送货有34分钟可用,应选哪种送货方式)


正确答案:
(1)选择电动车,由于方差比较小,更稳定一些。

答案解析:
本题考查正态分布。
12、简述不等式在中学数学课程中的作用。
正确答案:
“不等式”是中学数学重要内容,是数学基础理论的一个重要组成部分。在初中数学中,不等式的知识主要用以解决证明不等式、解不等式、应用不等式三类问题,因此不等式的性质是基础,是证明不等式和解不等式的理论依据。其性质及解法更体现在其它知识领域中的应用,如函数的定义域、单调性、最值、复数问题等等。 并且在数学教学中,数学思想方法是数学知识的精髓,也是联系各部分的纽带,我们始终贯穿着一个理念,那就是培养学生的数学思想方法。而不等式知识就是很好实践材料。如分类讨论、整体换元、数形结合、转化化归思想,这四种重要的数学思想方法的培养和渗透,完全可以借助不等式的教学来实现。 因此可以看出,在初中数学不等式的教学实践中我们也应该加强对不等式的研究,重视各种数学思想在不等式教学中应用。这也说明了不等式在高中数学中的重要地位和作用!
答案解析:
本题考查教学内容。
13、以“角平分线的性质定理”的教学为例,阐述数学定理教学的基本环节。
正确答案:


答案解析:
本题考查教学内容。
三、解答题
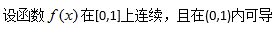
14、
正确答案:

答案解析:
本题考查微分学基本定理。
15、
正确答案:

答案解析:
本题考查微分学基本定理
四、简答题
16、函数单调性是刻画函数变化规律的重要概念,也是函数的一个重要性质。(1)请叙述函数严格单调递增的定义,并结合函数单调性的定义,说明中学数学课程中函数单调性与哪些内容有关(至少列举出两项内容)(7分)(2)请列举至少两种研究函数单调性的方法,并分别简要说明其特点。(8分)
正确答案:

答案解析:
本题考查课程内容。
五、案例分析题
在《有理数的加法》一节中.对于有理数加法的运算法则的形成过程,两位教师的一些教学环节分别如下:
【教师1】
第一步:教师直接给出几个有理数加法算式.引导学生根据有理数的分类标准,将加法算式分成六类,即:正数与正数相加,正数与负数相加,正数与0相加,0与0相加,负数与,0相加,负数与负数相加;
第二步:教师给出具体情境,分析两个正数相加、两个负数相加、正数与负数相加的情况;
第三步:让学生进行模仿练习;
第四步:教师将学生模仿练习的题目再分成四类:同号相加,一个加数是0,互为相反数的两个数相加,异号相加。分析每一类题目的特点,得到有理数加法法则。
【教师2】
第一步:请学生列举一些有理数加法的算式;
第二步:要求学生先独立运算,然后小组讨论,再全班交流。对于讨论交流的过程,教师提出具体要求:运算的结果是什么?你是怎么得到结果的?
……讨论过程中,学生提出利用其体情境来解释运算的合理性……
第三步:教师提出问题:“不考虑具体情境,基于不同情况分析这些算式的运算有哪些规律?”
……分组讨论后再全班交流,归纳得到有理数加法法则。
17、两位教师均重视分类讨论思想,简要说明并评价这两位教师关于分类讨论思想的教学方法的差异;(8分)
正确答案:
第一位教师的教学方法是典型的讲授法,从—开始便将分类的思想贯穿其中,教师直接给出几个有理数加法算式并引导学生利用以前学过的有理数的分类标准进行迁移,对有理数加法算式进行分类,能够使得学生快速地接受新知识,解决实际问题。
第二位教师在教学之初并没有强调分类的重要性,但是该教师能够以学生为主体,让学生列举一些有理数的加法的算式,充分调动了学生的主观能动性。再通过小组讨论,学生交流等过程,调动学生的学习积极性,给与了充分的时间与空间,对有理数加法进行讨论计算,有助于学生发散性思维的培养。
答案解析:
考查的教学设计。
18、请你再举两个分类讨论的例子,并结合你的例子谈谈对教学中的分类讨论思想及其教学的理解。(12分)
正确答案:

分类的过程就是对事物共性的抽象过程,在教学活动中要使学生逐步体会为什么要分类,如何分类,如何确定分类的标准。在分类过程中如何认识对象的性质,如何区别不同对象的不同性质。分类讨论是一种思想方法,需要滲透到学生的意识中,才能有效指导实践,渗透的过程不是一蹴而就的,而是需要在教学过程中,多次思考和长时间的积累才能将这种思维方式不断融入知识学习的各个阶段。
答案解析:
考查的教学方法。
六、教学设计题
《多边形的内角和》是八年级上册的内容,如何引导学生发现和推导出多边形内角和公式是该节课的重点。
19、如果将让学生体验“数学思考”作为该节课的一项教学目标,那么请列出该节课涉及的“数学思考的方法”。(8分)
正确答案:

答案解析:
本题考查数学思想方法。
20、请给出两种引导学生猜想四边形内角和的学生活动设计;(6分)
正确答案:

答案解析:
考查教学设计的活动设计
21、请列出两种证明四边形内角和的学生活动设计;(6分)
正确答案:

答案解析:
考查了教学设计中的证明设计。
22、某教师在《多边形的内角和》一节的教学中,设计了如下两个问题,你能说出我们为什么要研究四边形的内角和吗?你能基于四边形的内角和的证法,得到五边形、六边形,……,n边形内角和计算公式和证明方法吗?请分析该教师设计这两个问题的意图。(8分)
正确答案:
问题一设计意图:采用简单的四边形进行引导,利于学生迅速掌握知识,学生利用辅助线多角度的把多边形的内角和灵活地转化成三角形的内角和,体会转化的思想,并为下面五边形、六边形以及n边形的内角和做铺垫。
问题二设计意图:引导学生动手操作、动脑思考、小组讨论,从四边形到五边形再到六边形,以知识迁移的方式进一步体会将多边形分割成几个三角形的化归过程。也进一步明确了边数、对角线条数、三角形数对多边形内角和的影响,为从具体的多边形抽象到一般的n边形的研究奠定基础。
答案解析:
考查初中证明课题的教学设计。
喵呜刷题:让学习像火箭一样快速,快来微信扫码,体验免费刷题服务,开启你的学习加速器!








