一、单选题
1、

A 1
B 2
C 3
D 4
答案解析:

2、

A -39
B -13
C 13
D 39
答案解析:

3、

A 0
B 1
C 2
D ∞
答案解析:

4、

A
B
C
D
答案解析:

5、

A
B
C
D
答案解析:

6、

A
B
C
D
答案解析:

7、

A 旋转变换
B 勾股定理
C 杨辉三角图
D 数学进位制
答案解析:
本题主要考查数学史的相关知识。
A选项,主画面呈“S”型,体现了旋转变换,表示会议举办地在上海(Shanghai),并呈向前的动感,表示我们积极进取的态度。B选项,弦图是三国时期的数学家赵爽给出的勾股定理的一个绝妙证明,现在是中国数学会的徽标。D选项,主画面右下方标明“ICME-14”,它下方的“卦”是用中国古代八进制的计数符号写出的八进制数字3744,换算成10进制就是2020,表示开会的年份。从四个“卦”中也可以读出2020的二进制码:(0)11111100100。八进制和二进制把中国古代灿烂文明和现代科学技术联系在一起。因而选择C选项。
8、高中数学教学中的周期函数是( )
A 反三角函数
B 三角函数
C 对数函数
D 指数函数
答案解析:
本题考查了学科课程知识。高中数学教学中的周期函数是三角函数,故本题选B。
二、简答题
9、

正确答案:

答案解析:
本题考查行列式的求解和线性组合的相关知识。
10、

正确答案:

答案解析:
本题考查了定积分求平面面积。
11、

正确答案:

答案解析:
本题考查概率的相关知识。
12、学生能够获得进一步学习以及未来发展所必须的“四基”和“四能”是普通高中数学课程的要求之一,回答“四基”和“四能”分别是什么?
正确答案:
四基为基础知识、基本技能、基本思想、基本活动经验;四能为发现和提出问题的能力、分析和解决问题的能力。普通高中数学课程标准,在课程总目标中提出:通过高中数学课程的学习,学生能获得进一步学习以及未来发展所必需的数学基础知识、基本技能、基本思想、基本活动经验(简称“四基”)提高从数学角度发现和提出问题的能力、分析和解决问题的能力(简称“四能”)。
答案解析:
本题考查数学课程标准。
13、结合实例,简述什么是“简单随机抽样”和“分层随机抽样”。
正确答案:
一般地,设一个总体含有N个个体,如果通过逐个抽取的方法从中抽取一个样本,且每次抽取时各个个体被抽到的概率相等,则这样的抽样方法叫做简单随机抽样。简单随机抽样也称纯随机抽样。分层随机抽样,又称类型随机抽样,它是先将总体各单位按一定标准分成各种类型(或层);然后根据各类型单位数与总体单位数的比例,确定从各类型中抽取样本单位的数量;最后,按照随机原则从各类型中抽取样本。比如,我们要了解某市400个国营企业的生产经营情况,决定采取类型随机抽样法抽取20个企业作为样本进行调查,其具体做法是:首先,将这400个企业按产业(也可按行政区划、盈利情况、规模大小等)分为三类,假定第一产业40个,第二产业200个,第三产业160个。然后,按各类企业在总体中的比重,确定各类企业抽取样本单位的数量。其中,第一产业的企业占总体10%,按比例应抽样本企业2个;按同样方法计算,第二产业中应抽样本企业10个,第三产业中应抽样本企业8个。最后,采用简单随机抽样或等距随机抽样方法,从各类企业中抽出上述数量的样本单位。
答案解析:
本题考查概率与统计的数学学科知识。
三、解答题
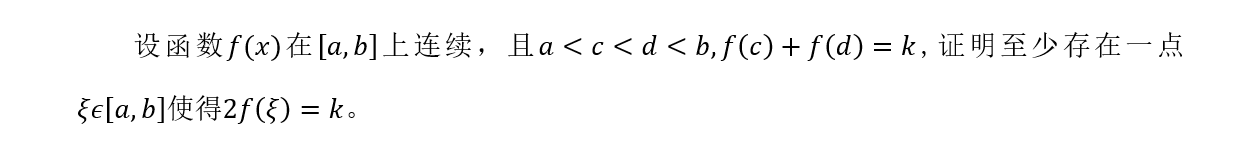
14、。
正确答案:

答案解析:
本题考查介值定理的应用。
四、简答题
15、函数是中学数学的重要内容,回答下列问题:(1)写出高中阶段函数的定义;(2)阐述高中阶段函数的定义与初中阶段函数定义的相同点和不同点。
正确答案:

答案解析:
本题考查中学数学函数的相关知识。
五、案例分析题

16、(1)指出这名学生在求解过程中的错误;(2)给出上述题目的正确解答过程;(3)结合此题的错误之处,分析这名学生在运算和逻辑推理方面的不足。
正确答案:

(3)《普通高中数学新课程标准(2017年版2020年修订)》指出,逻辑推理是得到数学结论、构建数学体系的重要方式,是数学严谨性的基本保证,是人们在数学活动中进行交流的基本思维品质,并且也指出数学运算是解决数学问题的基本手段。对于同角三角函数的基本关系,该同学虽然能够掌握基本公式,但是在运算过程中并没有注意到题干中的取值范围。而且在后面第⑤步的计算中也忽略了限定条件。因此需要去主动探究,积极思考,以养成良好的观察分析意识,全面提升自己的逻辑思维能力和运算能力。
答案解析:
本题考查数学学科知识、教学知识、课程标准。
六、教学设计题
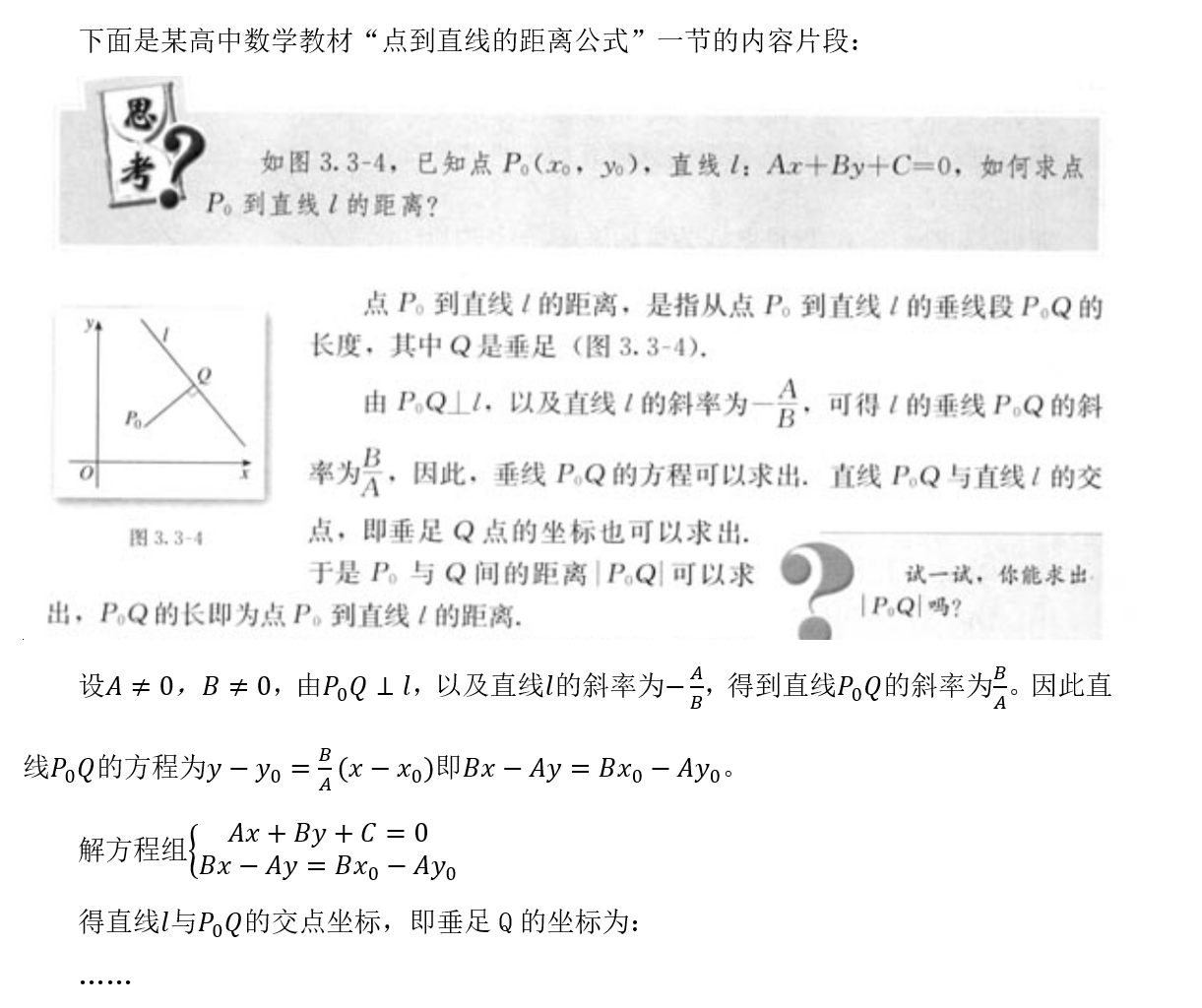
17、根据上述内容,完成下列任务:(1)补充“点到直线的距离公式”的证明过程;(10分)(2)设计这部分内容的教学目标;(8分)(3)根据教学目标设计这部分内容的数学过程(含课堂导入、公式推导、巩固提高、课堂小结及设计意图)(12分)
正确答案:

(2)知识与技能目标:理解点到直线距离公式的推导过程,掌握点到直线距离公式及其应用;过程与方法自标:通过合作交流,观察、思考、分析、归纳的过程,数学能力得到提高,数形结合、转化(或化归)等数学思想、特殊与一般的方法以及数学应用意识与能力能够得到发展。情感态度与价值观:用联系与转化的视角来看问题,了解和感受探索问题的方式方法,在探索问题的过程中获得成功的体验。
(3)教学过程如下
一、导入环节
多媒体显示实际的例子:某电信局计划年底解决本地区最后一个小区P的电话通信问题。离它最近的只有一条线路通过,要完成这项任务,至少需要多长的电缆?经过测量,若按照部门内部设计好的坐标图(以电信局为原点),得知这个小区的坐标为P(-1,5),离它最近线路其方程为2x+y+10=0。教师提问:这个实际问题要解决,要转化成什么样的数学问题?学生得出就是求点到直线的距离。教师提出这堂课我们就来学习点到直线的距离,并板书课题:点到直线的距离。
【设计意图】通过抛出实际生活中的问题,激发学生思考,吸引学生的注意力,同时也让学生意识到数学来源于生活并运用于生活。

【设计意图】对于公式的教学,并不是仅仅将公式交给学生,而是要引导学生不断思考,通过自己的不断探索从而得出结论。这样既能体现新课标的以学生为主体的理念,也能更好地帮助学生掌握知识。

答案解析:
本题考查教学设计。
喵呜刷题:让学习像火箭一样快速,快来微信扫码,体验免费刷题服务,开启你的学习加速器!







