一、单选题
1、极限的值是（ ）。
A 0
B 1
C
D 不存在
答案解析：
=0
2、空间曲面xyz=1被平面x=1截得的曲线是()
A 圆
B 椭圆
C 抛物线
D 双曲线
答案解析：
根据题意可知，yz=1,故表是在yOZ平面内的等轴双曲线。
3、矩阵A=的行向量组的极大线性无关组所含向量的个数是（）
A
B 2
C 3
D 4
答案解析：
对于矩阵进行变换可得R（A）=4，所以该向量组是线性无关的，即矩阵A的向量组的极大线性无关组所含向量的个数是4
4、直线与平面4x-2y-2z=3的位置关系（）
A
B
C
D 相交但不垂直
答案解析：
直线的方向向量为（-2，-7,3），平面的法向量为（4，-2，-2）因为两个向量相乘的积等于0，且直线上的点（-3，-4,0）不在平面上，所以平行。
5、已知函数f(x)=，则f(x)在点x=0处（）
A
B
C
D 二阶可导
答案解析：
6、.已知球面方程为在z轴上取一点P作球面的切线与球面相切于点M，线段PM长为，则在点P的坐标（0，0，z）中，z的值为（ ）
A
B 2
C 3
D 4
答案解析：
因为M为切点，所以OM=1，由PM长为
结合勾股定理知OP=3，故z=3。
7、
A 抽象概括能力
B 运算求解能力
C 推理论证能力
D 数据处理能力
答案解析：
依据题意可得，从已知条件出发求解cos2θ的过程主要考查的是学生的运算求解能力。故本题选B
8、如图：
A 推广，类比，特殊化
B 特殊化，推广，类比
C 推广，特殊化，类比
D 类比，特殊化，推广
答案解析：
经历由平面向量推到空间向量的过程，了解空间向量的概念，经历由平面向量方法及其法则类比到空间向量的过程，所以(1)是类比;由向量何法向代数几何法的过渡是一种特殊化的法，故(2)是特殊化；向量几何法实质是有向线段的运算，推广此方法延伸到数轴与向量，（3）应该是推广。
二、简答题
9、
正确答案：
答案解析：
本题主要考查均值不等式
10、设A是3×4矩阵，其秩为3，已知是非齐次线性方程组AX=b的两个不同的解，其中x=，b=求（1）AX=0的解（2）AX=b的解
正确答案：
（1）因为未知数个数为4，而系数矩阵A是3X4矩阵，其秩为3，故Ax=0的自由未知量个数为1，可设Ax=0的基础解系为η，所以Ax=b的解的构成为Ax=0的基础解系加一个Ax=b的特解，所以
=
=kη+
。所以kη=
-
，故Ax=0的解就是k(
-
),
答案解析：
本题主要考查线性方程组
11、
正确答案：
答案解析：
本题主要考查概率
12、简述为什么函数是普通高中数学课程的主线之一
正确答案：
函数思想是贯穿整个高中数学课程始终的重要思想之一。为了更好的理解高中数学课程，需要弄清中、小学数学课程中函数思想的发展脉络。（1）在高中阶段，学习的知识更加丰富了。我们利用更丰富的实例引导学生认识到，函数是刻画日常生活和其他学科规律的重要数学模型。在高中数学中，函数模型应该占有很重要的地位。我们在任何一个生活情景中，例如，邮局、加油站、机场等等，都会发现许多描述规律的函数关系。在其他学科，如物理、化学、生物、地理、社会、经济等学科中，描述规律的函数关系比比皆是。因此函数的基础知识在现实生活、社会、经济及其他学科中有着广泛的应用;函数的观点和方法贯穿整个高中代数的全过程，又渗透到立体几何和解析几何中.（2）知道了函数的定义之后，再去研究它的性质。我们先让学生认识一些具体函数的模型，例如，分段函数，简单的幂函数、指数函数与对数函数、三角函数。结合这些函数，我们引入了刻画函数变化的单调性、周期性、奇偶性等基本的性质。可以让学生体验“实际问题一建立数学模型一数学解答一实际问题的解”的问题解决模式，深化对函数概念的理解.（3）函数的思想在其他部分数学内容的学习中发挥着重要作用。在高中课程中，函数与数列、函数与导数及其应用、函数与算法、函数与概率中的随机变量等都有着密切的联系。用函数(映射)的思想去理解这些内容，是非常重要的一个出发点，反过来，通过这些内容的学习，更加深了对于函数思想的认识。综上所述，函数思想是高中数学课程的一条主线，从一个角度链接起了高中数学课程的许多内容.
答案解析：
本题主要考查函数课程理解
13、简述数学运算的基本内涵。
正确答案：
数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养。主要包括：理解运算对象，掌握运算法则，探究运算思路，选择运算方法，设计运算程序，求得运算结果等。例如：二项式定理的学习中，根据多项式相乘的运算法则，探索：二项式的构造证明，体会运算法则的作用的同时，感知运算不仅是一种严格的逻辑推理，通过一般性的运算发现和提出命题，掌握推理的基本形式和规则，探索和表述论证的过程，不仅提高推理能力，也发展了数学运算素养
答案解析：
本题主要考查数学运算的内涵
三、解答题
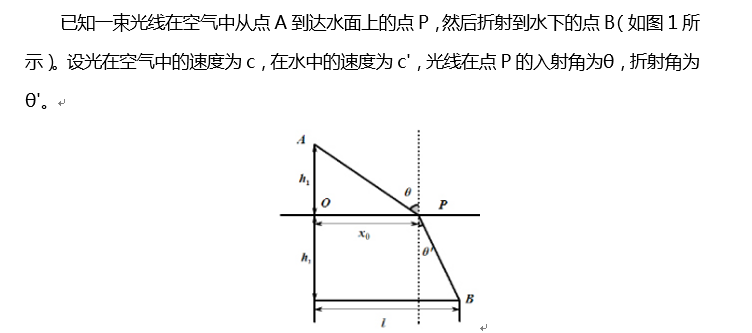
14、（1）若OP长为x0，请写出光线从点A到达点B所需时间T(x0)的表达式；（6分）
正确答案：
答案解析：
略
15、（2）若T(x0)是光线由点A到达点B所需时间的极小值，证明sinθ/(sinθ' )=c/c'
正确答案：
答案解析：
略
四、简答题
16、伴随着大数据时代的到来，数据分析已经深入到现代社会生活的各个方面，结合实例阐述在中学数学的教学中培养学生的数据分析能力的意义
正确答案：
数学来源于生活，生活离不开数学。学生在学习数学的过程中，知识的获取固然重要，在获取知识的过程中，培养学生生成智慧，发展学生思维能力，让学生形成数据分析观念，用数学的眼光看待解决问题，这才是根本。学生数据分析观念的培养都离不开对生活中的数学问题的探究。这就要求我们培养学生的数据分析观念，以数学的眼光解决一些实际问题。学生数据观念的培养，就是通过解决生活中的实际问题来实现的，最终以问题的解决为目的。高中数学课程改革着力于发展学生的数学核心素养，数据分析能力作为六大核心素养之一至关重要.通过高中数学课程的学习，学生能提升获取有价值信息并进行定量分析的意识和能力;适应数字化学习的需要，增强基于数据表达现实问题的意识，形成通过数据认识事物的思维品质，积累依托数据探索事物本质、关联和规律的活动经验.
答案解析：
本题主要考查数据分析
五、案例分析题
在基本不等式: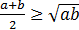 
∈R+，(R+表示全体正实数的集合)当且仅当a=b时等号成立的教学中，两位教师创设了如下情境:
情境1:某商店在双十一进行商品降价促销活动，拟分两次降价，有三种降价方案;甲方案是第一-次打P折销售，第二次打Q折销售;乙方案是第一次打Q折销售，第二次打P折销售;丙方案是两次都打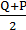
折销售，请问哪一次降价最多?
情境2:现有一台天平两臂之长略有差异，其他均精确，有人要用他称量物质的量，只需将物体放在左右两个托盘中各称一次，再将称量结果相加后除以2，就是物体的真实质量，你认为这种做法对不对?如果不对的话，你能否找到一种用这台天平量物体质量的正确做法?
17、请对上述的两种情景创设给予评价(10分)
正确答案：
情景1中，老师通过现实生活中的打折例子创设情景，将教材内容与生活情景有机的结合起来，使数学知识成为学生看得见、听得到、摸得着的现实.只要善于挖掘数学内容中的生活情景，让数学贴近生活，学生就会真正的体会到生活充满了数学，感受到数学的真谛，从而增强对学好数学的信心，学会用数学的眼光看世界，感受数学无处不在，进而培养学生的创新思维.情景2中，通过数学应用性问题创设情景，将数学问题深加工，建立一种物理问题的模型，贴近生活，贴近实际，给学生创设了一个观察、联想、抽象、概括、数学化的过程.数学应用性问题不仅能激发兴趣，培养学生追溯问题的背景和原型，还能使其思维发散、个性发展，形成分析问题和解决问题的能力，提高的数学的应用能力，这是数学素养教育的要求，是新课改的要求.在这样的问题情境下，给学生动手、动脑的空间和时间，学生一定会想学、乐学、主动学.
答案解析：
本题主要考查教学评价
18、数学教学中情境创设应该注意哪些问题?:(10分)
正确答案：
1.要明确情景导入的目的和针对性。教师要明确导入教学的目的。无论采用何种导入方式都应使设置的问题情景指向教学目标。通过导入教学活动，应该使学生初步明确学习的内容是什么，为什么学，怎么学。针对性是要针对教学内容，所设计的导语与教学内容构成有机的内在联系，不可游离于教学内容之外，还要针对学生的年龄特点、心理状况、知识基础、能力水平、兴趣差异等实际情况设计导语。2.要重视关联和递进性。运用导入的各种方法时，要注意学科教材本身的系统性。要以旧知识为前提，以旧拓新，温故知新，使导语的内容提要与新课的重点紧密结合，揭示新旧知识的内在联系，使旧知识通过新知识得到扩展和深化。3.要体现直观性和启发性。要尽量以生动、具体的事例为基础导入新知识，同时要讲究启发性，要让学生从浅显简明的事例中发现问题，进而从问题着手，此起学生认知冲突，激发其积极思维和产生寻求解决问题的方法的强烈愿望。4.要富有趣味性和艺术性。情景导入不仅要新颖独特、引人入胜，以新鲜活泼的面貌出现在学生面前，令学生耳目一新，而且要有风趣，通过充满情趣的导入，调剂课堂教学的气氛和节奏，最大限度地引起学生的兴趣，激发学生的积极性。5.要具有简洁性和灵活性。导入仅是一个“引子”，而不是内容铺开的讲授，故导入的时间不宜过长，一般以3---分钟为宜。所以要求导语要短小精练、简洁，尽可能在最短的时间内完成导入，最大限度地提高课堂效率。在导入方式上，要根据教学实际，既灵活多样，又讲究综合。不能老用一种模式，谨防学生发生兴趣抑制。
答案解析：
本题主要考查情景导入的原则
六、教学设计题
二分法是运用函数性质求方程近似解的基本方法，为了帮助学生掌握二分法《普通高中数学课程标准(2017 年版)》提出的学习要求是:1:结合学过的函数图像，了解函数零点与方程解的关系;2:结合具体连续函数及其图像特点，了解函数零点存在定理，探索用二分法求方程近似解的思路，并会画程序框图，能借助计算工具用二分法求方程近似解，了解用二分法求方程近似解的般性。四请以达到学习要求2为目的，设计“二分法”的一个教学方案，要求:
19、写出明确的教学重点(6分)
正确答案：
通过用二分法求方程的近似解，体会函数的零点与方程根之间的联系，初步形成用函数观点处理问题的意识．
答案解析：
重难点
20、设计主要的教学环节(问题导入、二分法生成过程、巩固新知识)及其设计意图(24分)
正确答案：
答案解析：
教学设计
喵呜刷题：让学习像火箭一样快速，快来微信扫码，体验免费刷题服务，开启你的学习加速器！
