一、单选题
1、

A 0
B 1
C
D
答案解析:
本题考查极限的求法中的两个常见公式

2、下列命题中正确的是( )
A 若n阶行列式D=0,那么D中有两行元素相同
B 若n阶行列式D=0,那么D中有两行元素对应成比例
C
D
答案解析:
本题考查行列式的性质,行列式中有两行相等或者两行对应成比例,那么行列式的值为0。
3、

A 平行
B 直线在平面内
C 垂直
D 相交但不垂直
答案解析:
本题考查直线与平面的位置关系,利用空间向量来进行判断。
该直线是两个平面的交线,直线的方向向量垂直于两个平面的法向量。因此在求方向向量时,可以根据空间向量的向量积来求。

4、

A
B
C
D
答案解析:
本题考查函数在某点处连续。
根据函数在某点处连续的定义可知,选A。
5、

A -2
B 2
C
D
答案解析:
本题考查特征值特征向量的求法。

6、

A
B
C
D
答案解析:
本题考查离散型随机变量的方差。
由离散型随机变量的方差公式可知,选B
7、数学发展史上曾经历过三次危机,触发第三次数学危机的事件是( )
A 无理数的发现
B 微积分创立
C 罗素悖论
D 数学命题的机器证明
答案解析:
本题考查数学史的知识。
三次数学危机分别是:无理数的发现、微积分的创立和罗素悖论。
8、在某次测试中,用所有参加测试学生某题的平均分除以该题分值,得到的结果是( )
A 区分度
B 难度
C 信度
D 效度
答案解析:
本题考查数学测验的统计指标
区分度是指考试题目对考生心理特征的区分能力。区分度高的试题能将不同水平的考生区分开来,水平高的考生得高分,水平低的考生得低分。区分度高的考试,优秀、一般、差三个层次的学生都有一定比例,如果某一分数区间学生相对集中,高分太多或不及格太多的考试,区分度则低。排除A。
信度是指使用同一试卷对考生重复测验时,或两个平行试卷对考生测验时,所得测验分数的一致性和稳定性程度。信度除了要说明成绩的真实性之外,还要说明题目涉及的内容与教学的相关程度。排除C.
效度是指考试有效性或正确性的质量指标,即是否考了要考的内容,试题难度、区分度是否适宜,考试最终是否达到了它的预定目的等。排除D。
难度是指试题的难易程度,是评价考试的一个非常重要的一个指标。一个题目,如果大部分考生都能答对,那么这个题目的难度就小;如果大部分考生都不能答对,那么这个题目的难度就大。用所有参加测试学生某题的平均分除以该题分值,得到的结果就是难度。所以选B。
二、简答题
9、

正确答案:

答案解析:
本题考查线性变换的知识
10、

正确答案:

答案解析:
本题考查非齐次线性方程组有解的条件以及解的求法
11、王强是一位快递员,他负责由A到B地的送货任务,送货方式为开汽车或者电动车,他分别记录了开汽车和骑电动车各100次所用的送货时间,经过数据分析得到如下数据:开汽车:平均用时24分钟,方差为36;骑电动车:平均用时34分钟,方差为4.(1)根据上述数据,你会建议王强选择哪种送货方式?请说明理由(3分)(2)分别用X和Y表示开汽车和骑电动车所用的时间,X和Y的分布密度曲线如图所示(假设这些曲线具有轴对称性,为达到准时送达的目的,如果某次送货有38分钟可用,应该选择哪种送货方式?如果某次送货有34分钟可用,应选哪种送货方式)

正确答案:

答案解析:
本题考查正态分布的知识
12、简述不等式在中学数学课程中的作用。
正确答案:
“不等式”是中学数学重要内容,是数学基础理论的一个重要组成部分。在高中数学中,不等式的知识主要用以解决证明不等式、解不等式、应用不等式三类问题,因此不等式的性质是基础,是证明不等式和解不等式的理论依据。其性质及解法更体现在其它知识领域中的应用,如函数的定义域、单调性、最值、复数问题等等。 并且在数学教学中,数学思想方法是数学知识的精髓,也是联系各部分的纽带,我们始终贯穿着一个理念,那就是培养学生的数学思想方法。而不等式知识就是很好实践材料。如分类讨论、整体换元、数形结合、转化化归思想,这四种重要的数学思想方法的培养和渗透,完全可以借助不等式的教学来实现。 因此可以看出,在高中数学不等式的教学实践中我们也应该加强对不等式的研究,重视各种数学思想在不等式教学中应用。这也说明了不等式在高中数学中的重要地位和作用!
答案解析:
本题考查高中数学的内容
13、以“二项式定理”的教学为例,阐述数学定理及教学的基本特征。
正确答案:





答案解析:
本题考查数学命题教学
三、解答题
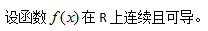
14、
正确答案:

答案解析:
本题考查导数的相关知识
15、
正确答案:

答案解析:
本题考查微分学基本定理
四、简答题
16、函数单调性是刻画函数变化规律的重要概念,也是函数的一个重要性质。(1)请叙述函数严格单调递增的定义,并结合函数单调性的定义,说明中学数学课程中函数单调性与哪些内容有关(至少列举出两项内容)(7分)(2)请列举至少两种研究函数单调性的方法,并分别简要说明其特点。(8分)
正确答案:

答案解析:
本题考查函数的基本性质。
五、案例分析题

17、结合上述案例,谈谈教师应如何看待学生提问不在教学预设的情况(10分)
正确答案:
(1) 教学中的预设,表现在课堂上,指的是师生教学活动按照教师课前的设计和安排展开,课堂教学活动按计划有序进行。而生成则是指在教师与学生、学生与学生合作、交流、碰撞的课堂中,现时生成的超过教师预设方案之外的新问题、新情况或新资源。新课改理念的实施,给了学生们广阔的发展空间,课上学生可以自由地提出自己的问题,如果对课堂上有着不同智力水平、知识经验、认知风格和情感表达的学生所提出的的问题都一一回应,课将无法进行。但如果对学生的问题全部忽视也不可取,应当区别对待,恰当应对学生的课堂提问。
在课堂中,要处理好学生提问不在教学预设的情况下,还要注意恰当地选择处理方法,可以直接告诉学生答案,也可以师生互动讨论,可以是学生自行探究,也可以请学生课下解决。所以,教师要恰当回应学生的课堂提问,并非一件易事,它需要有把学生提出的问题以课堂教学资源来看待的意识,并且要有判断问题价值的能力和灵活的调控教学环节的能力。所以教师要不断地学习、研究,不断地进行自我反思,不断地进行经验的积累。
答案解析:
本题考查课堂中“预设”与“生成”的关系
18、如果你是该老师,那么如何回答学生的提问?(10分)
正确答案:
如果我是该教师我会进行小组讨论,将学生前后四人为一个小组,给学生5分钟的时间,请学生小组讨论一下。随后,请学生代表进行结果展示。

对比三种解决方法,各自的优点是什么?
引导学生共同总结:在解决三角函数公式证明题的时候,合理的选择诱导公式以及和差化积公式非常重要,要灵活的运用整理代换的思想方法快速解决问题。
答案解析:
本题考查教学设计
六、教学设计题
“对数的概念”是高中数学教材的重要概念,教师在教学中,应基于课程标准和学生学情,确定教学目标,实现教学重点、突破教学难点,设计教学方法,教学过程中,师生互动和教学评价等,请完成下列任务。
19、设计“对数的概念”的教学目标(9分)
正确答案:
(1)知识与技能目标:理解对数的概念,了解对数运算与指数运算的互逆关系,掌握对数的运算性质,并且进行能进行对数运算。
过程与方法目标:通过实例引出对数问题,培养分析转化的意识,培养逆向思维。
情感态度与价值观目标:通过与指数的类比以及对数概念的学习,树立事物发展的辩证发展和矛盾转化的观点,培养严谨的治学态度。
答案解析:
本题考查教学设计
20、写出“对数的概念”的教学重点和难点(6分)
正确答案:
(2)教学重点:对数式与指数式的互化以及对数的性质
教学难点:对数概念的理解
答案解析:
本题考查教学设计
21、写出“对数的概念”的引入过程(要求能够让学生认识到引入对数概念的必要性)(15分)
正确答案:

答案解析:
本题考查教学中的导入环节的设计
喵呜刷题:让学习像火箭一样快速,快来微信扫码,体验免费刷题服务,开启你的学习加速器!







