一、实操题
1、铺地毯
【问题描述】
为了准备一个独特的颁奖典礼,组织者在会场的一片矩形区域(可看做是平面直角坐标系的第一象限)铺上一些矩形地毯。一共有 n 张地毯,编号从 1 到 n。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设,后铺的地毯覆盖在前面已经铺好的地毯之上。地毯铺设完成后,组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意:在矩形地毯边界和四个顶点上的点也算被地毯覆盖。
【输入】
输入文件名为 carpet.in。
输入共 n+2 行。
第一行,一个整数 n,表示总共有 n 张地毯。
接下来的 n 行中,第 i+1 行表示编号 i 的地毯的信息,包含四个正整数 a,b,g,k,每两个整数之间用一个空格隔开,分别表示铺设地毯的左下角的坐标(a,b)以及地毯在 x轴和 y 轴方向的长度。
第 n+2 行包含两个正整数 x 和 y,表示所求的地面的点的坐标(x,y)。
【输出】
输出文件名为 carpet.out。
输出共 1 行,一个整数,表示所求的地毯的编号;若此处没有被地毯覆盖则输出-1。
【输入输出样例 1】
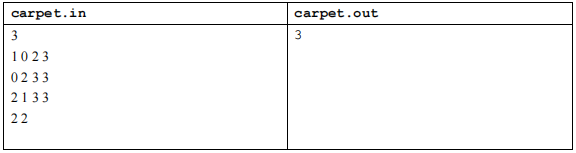
【输入输出样例说明】
如下图,1 号地毯用实线表示,2 号地毯用虚线表示,3 号用双实线表示,覆盖点(2,2)的最上面一张地毯是 3 号地毯。
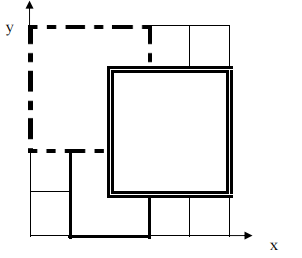
【输入输出样例 2】
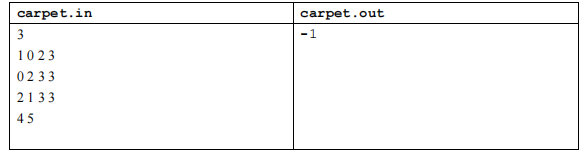
【输入输出样例说明】
如上图,1 号地毯用实线表示,2 号地毯用虚线表示,3 号用双实线表示,点(4,5)没有被地毯覆盖,所以输出-1。
【数据范围】
对于 30%的数据,有 n≤2;
对于 50%的数据,0≤a, b, g, k≤100;
对于 100%的数据,有 0≤n≤10,000,0≤a, b, g, k≤100,000。
参考答案:根据题目描述,我们需要模拟铺设地毯的过程,并判断指定点是否被地毯覆盖。具体步骤如下:1. 读取输入数据,包括地毯的数量n和每张地毯的左下角坐标(a, b)以及地毯在x轴和y轴方向的长度(g, k)。2. 初始化一个二维数组dp,用于记录每个点是否被地毯覆盖。dp[i][j]表示点(i, j)是否被地毯覆盖,初始值为0。3. 遍历每张地毯,按照编号从小到大的顺序依次铺设。对于每张地毯,遍历其覆盖的所有点,并将dp数组对应位置的值设为当前地毯的编号。4. 读取指定的点(x, y),判断该点是否被地毯覆盖。如果dp[x][y]的值不为0,则输出dp[x][y]的值;否则输出-1。
2、选择客栈
【问题描述】
丽江河边有 n 家很有特色的客栈,客栈按照其位置顺序从 1 到 n 编号。每家客栈都按照某一种色调进行装饰(总共 k 种,用整数 0 ~ k-1 表示),且每家客栈都设有一家咖啡店,每家咖啡店均有各自的最低消费。
两位游客一起去丽江旅游,他们喜欢相同的色调,又想尝试两个不同的客栈,因此决定分别住在色调相同的两家客栈中。晚上,他们打算选择一家咖啡店喝咖啡,要求咖啡店位于两人住的两家客栈之间(包括他们住的客栈),且咖啡店的最低消费不超过 p。
他们想知道总共有多少种选择住宿的方案,保证晚上可以找到一家最低消费不超过 p元的咖啡店小聚。
【输入】
输入文件 hotel.in,共 n+1 行。
第一行三个整数 n,k,p,每两个整数之间用一个空格隔开,分别表示客栈的个数,色调的数目和能接受的最低消费的最高值;
接下来的 n 行,第 i+1 行两个整数,之间用一个空格隔开,分别表示 i 号客栈的装饰色调和 i 号客栈的咖啡店的最低消费。
【输出】
输出文件名为 hotel.out。
输出只有一行,一个整数,表示可选的住宿方案的总数。
【输入输出样例 1】

【输入输出样例说明】
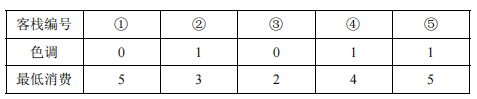
2 人要住同样色调的客栈,所有可选的住宿方案包括:住客栈①③,②④,②⑤,④⑤,
但是若选择住 4、5 号客栈的话,4、5 号客栈之间的咖啡店的最低消费是 4,而两人能承受的最低消费是 3 元,所以不满足要求。因此只有前 3 种方案可选。
【数据范围】
对于 30%的数据,有 n≤100;
对于 50%的数据,有 n≤1,000;
对于 100%的数据,有 2≤n≤200,000,0<k≤50,0≤p≤100, 0≤最低消费≤100。
参考答案:根据题目描述,我们需要计算满足条件的住宿方案总数。我们可以使用动态规划的方法来解决这个问题。首先,我们定义一个数组dp[i][j],其中i表示当前考虑到的客栈的编号,j表示当前选择的色调。dp[i][j]表示以i号客栈为结尾,色调为j的满足条件的住宿方案数。然后,我们遍历每个客栈,对于每个客栈,我们遍历它的前一个客栈,如果前一个客栈的色调和当前客栈的色调相同,并且前一个客栈和当前客栈之间的咖啡店的最低消费不超过p,那么我们就可以将dp[i-1][j]累加到dp[i][j]上。最后,我们遍历所有的色调,将dp[n][j]累加起来,就可以得到总的满足条件的住宿方案数。
3、Mayan 游戏
【问题描述】
Mayan puzzle 是最近流行起来的一个游戏。游戏界面是一个 7 行 5 列的棋盘,上面堆放着一些方块,方块不能悬空堆放,即方块必须放在最下面一行,或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块,消除方块的规则如下:
1、 每步移动可以且仅可以沿横向(即向左或向右)拖动某一方块一格:当拖动这一方块时,如果拖动后到达的位置(以下称目标位置)也有方块,那么这两个方块将交换位置(参见输入输出样例说明中的图 6 到图 7);如果目标位置上没有方块,那么被拖动的方块将从原来的竖列中抽出,并从目标位置上掉落(直到不悬空,参见下面图 1 和图 2);
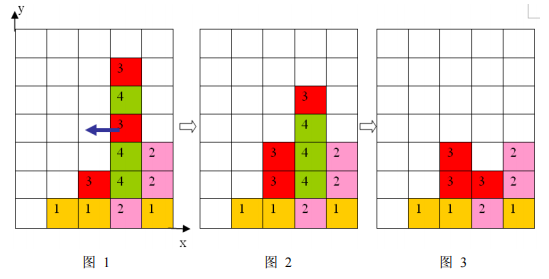
2、 任一时刻,如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块,则它们将立即被消除(参见图 1 到图 3)。
注意:
a) 如果同时有多组方块满足消除条件,几组方块会同时被消除(例如下面图 4,三个颜色为 1 的方块和三个颜色为 2 的方块会同时被消除,最后剩下一个颜色为 2 的方块)。
b) 当出现行和列都满足消除条件且行列共享某个方块时,行和列上满足消除条件的所有方块会被同时消除(例如下面图 5 所示的情形,5 个方块会同时被消除)。

3、 方块消除之后,消除位置之上的方块将掉落,掉落后可能会引起新的方块消除。注意:掉落的过程中将不会有方块的消除。
上面图 1 到图 3 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为(0, 0),将位于(3, 3)的方块向左移动之后,游戏界面从图 1 变成图 2 所示的状态,此时在一竖列上有连续三块颜色为 4 的方块,满足消除条件,消除连续 3 块颜色为 4 的方块后,上方的颜色为 3 的方块掉落,形成图 3 所示的局面。
【输入】
输入文件 mayan.in,共 6 行。
第一行为一个正整数 n,表示要求游戏通关的步数。
接下来的 5 行,描述 7*5 的游戏界面。每行若干个整数,每两个整数之间用一个空格隔开,每行以一个 0 结束,自下向上表示每竖列方块的颜色编号(颜色不多于 10 种,从 1 开始顺序编号,相同数字表示相同颜色)。
输入数据保证初始棋盘中没有可以消除的方块。
【输出】
输出文件名为 mayan.out。
如果有解决方案,输出 n 行,每行包含 3 个整数 x,y,g,表示一次移动,每两个整数之间用一个空格隔开,其中(x,y)表示要移动的方块的坐标,g 表示移动的方向,1 表示向右移动,-1 表示向左移动。注意:多组解时,按照 x 为第一关健字,y 为第二关健字,1优先于-1,给出一组字典序最小的解。游戏界面左下角的坐标为(0,0)。
如果没有解决方案,输出一行,包含一个整数-1。
【输入输出样例 1】
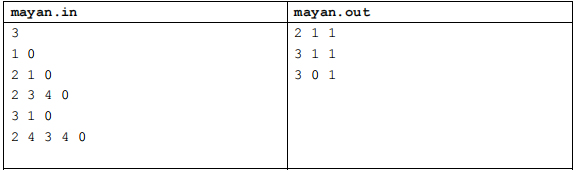
【输入输出样例说明】
按箭头方向的顺序分别为图 6 到图 11
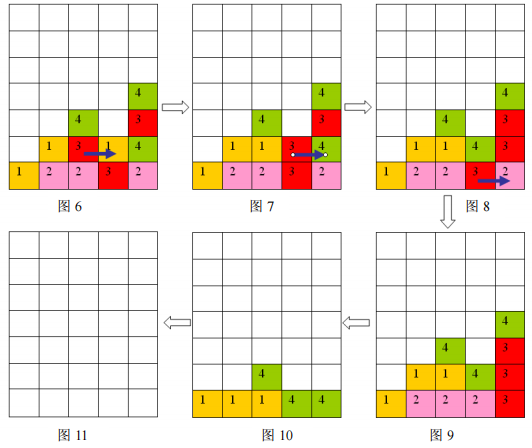
样例输入的游戏局面如上面第一个图片所示,依次移动的三步是:(2,1)处的方格向右移动,(3,1)处的方格向右移动,(3,0)处的方格向右移动,最后可以将棋盘上所有方块消除。
【数据范围】
对于 30%的数据,初始棋盘上的方块都在棋盘的最下面一行;
对于 100%的数据,0 < n≤5。
参考答案:br />-1
喵呜刷题:让学习像火箭一样快速,快来微信扫码,体验免费刷题服务,开启你的学习加速器!








