一、实操题
1、数字游戏
【问题描述】
小K同学向小P同学发送了一个长度为8的 01字符串来玩数字游戏，小P 同学想 要知道字符串中究竟有多少个1。
注意：01字符串为每一个字符是0或者1的字符串，如“101”(不含双引号)为一 个长度为3的01字符串。
【输入格式】
输入文件名为number in。
输入文件只有一行， 一个长度为8的01字符串s。
【输出格式】
输出文件名为number.out。
输出文件只有一行，包含一个整数，即01字符串中字符1 的个数。
【输入输出样例1】
【输入输出样例1说明】
该01字符串中有2个字符1。
【输入输出样例2】
【输入输出样例2说明】
该01字符串中有8个字符1。
【数据规模与约定】
对于20%的数据，保证输入的字符全部为0。
对于100%的数据，输入只可能包含字符0和字符1,字符串长度固定为8。
参考答案：对于输入的01字符串，我们需要统计其中字符1的个数。可以直接遍历字符串，对每个字符进行判断，如果是字符1，则计数器加1。最后输出计数器的值即可。
2、公交换乘
【问题描述】
著名旅游城市B市为了鼓励大家采用公共交通方式出行，推出了一种地铁换乘公交 车的优惠方案：
1.在搭乘一次地铁后可以获得一张优惠票，有效期为45分钟，在有效期内可以 消耗这张优惠票，免费搭乘一次票价不超过地铁票价的公交车。在有效期内指 开始乘公交车的时间与开始乘地铁的时间之差小于等于45分钟，即：tbus-tsubway≤45
2. 搭乘地铁获得的优惠票可以累积，即可以连续搭乘若干次地铁后再连续使用优 惠票搭乘公交车。
3. 搭乘公交车时，如果可以使用优惠票一定会使用优惠票；如果有多张优惠票满 足条件，则优先消耗获得最早的优惠票。
现在你得到了小轩最近的公共交通出行记录，你能帮他算算他的花费吗?
【输入格式】
输入文件名为transfer . in。
输入文件的第一行包含一个正整数n,代表乘车记录的数量。
接下来的n行，每行包含3个整数，相邻两数之间以一个空格分隔。第i行的 第1个整数代表第i条记录乘坐的交通工具，0代表地铁，1代表公交车；第2个 整数代表第i条记录乘车的票价pricei;第三个整数代表第i条记录开始乘车的时 间ti (距0时刻的分钟数)。
我们保证出行记录是按照开始乘车的时间顺序给出的，且不会有两次乘车记录出现 在同一分钟。
【输出格式】
输出文件名为transfer . out。
输出文件有一行，包含一个正整数，代表小轩出行的总花费
【 输入输出样例 1】
【输入输出样例1说明】
第一条记录，在第3分钟花费10元乘坐地铁。
第二条记录，在第46分钟乘坐公交车，可以使用第一条记录中乘坐地铁获得的优 惠票，因此没有花费。
第三条记录，在第50分种花费12元乘坐地铁。
第四条记录，在第96分钟乘坐公交车，由于距离第三条记录中乘坐地铁已超过45 分钟，所以优惠票已失效，花费3元乘坐公交车。
第五条记录，在第110分钟花费5元乘坐地铁。
第六条记录，在第135分钟乘坐公交车，由于此时手中只有第五条记录中乘坐地铁 获得的优惠票有效，而本次公交车的票价为6元，高于第五条记录中地铁的票价5元， 所以不能使用优惠票，花费6元乘坐公交车。
总共花费36元。
【输入输出样例2】
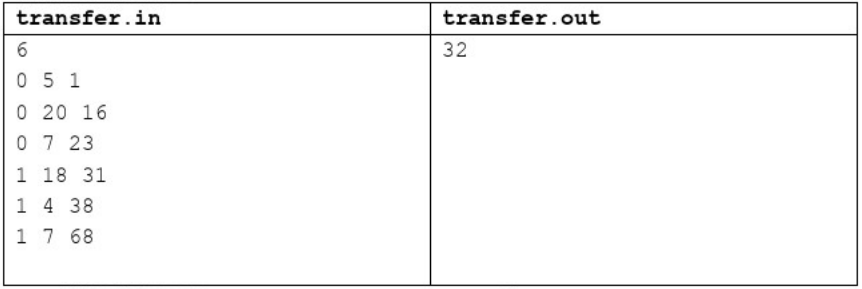
【输入输出样例2说明】
第一条记录，在第1分钟花费5元乘坐地铁。
第二条记录，在第16分钟花费20元乘坐地铁。
第三条记录，在第23分钟花费7元乘坐地铁。
第四条记录，在第31分钟乘坐公交车，此时只有第二条记录中乘坐的地铁票价高 于本次公交车票价，所以使用第二条记录中乘坐地铁获得的优惠票。
第五条记录，在第38分钟乘坐公交车，此时第一条和第三条记录中乘坐地铁获得 的优惠票都可以使用，使用获得最早的优惠票，即第一条记录中乘坐地铁获得的优惠票。
第六条记录，在第68分钟乘坐公交车，使用第三条记录中乘坐地铁获得的优惠票。 总共花费32元。
【数据规模与约定】
参考答案：根据给定的输入，我们需要模拟小轩的公共交通出行记录，并计算他的总花费。首先，我们需要维护一个时间戳和一个优惠票列表。时间戳记录当前时间，优惠票列表存储每张优惠票的信息，包括获得时间、地铁票价和有效时间。对于每条记录，我们按照以下步骤处理：1. 如果记录是地铁，则更新时间戳，并将优惠票加入优惠票列表。2. 如果记录是公交车，则遍历优惠票列表，找到最早获得且满足有效时间的优惠票，如果找到，则使用优惠票免费搭乘公交车，并从优惠票列表中移除该优惠票；否则，需要支付公交车票价。3. 更新时间戳。最后，计算总花费并输出。
3、纪念品
【问题描述】
小伟突然获得一种超能力，他知道未来T天N种纪念品每天的价格。某个纪念品 的价格是指购买一个该纪念品所需的金币数量，以及卖出一个该纪念品换回的金币数量。
每天，小伟可以进行以下两种交易无限次：
1. 任选一个纪念品，若手上有足够金币，以当日价格购买该纪念品；
2. 卖出持有的任意一个纪念品，以当日价格换回金币。
每天卖出纪念品换回的金币可以立即用于购买纪念品，当日购买的纪念品也可以当 日卖出换回金币。当然， 一直持有纪念品也是可以的。
T天之后，小伟的超能力消失。因此他一定会在第T天卖出所有纪念品换回金币。 小伟现在有M枚金币，他想要在超能力消失后拥有尽可能多的金币。
【输入格式】
输入文件名为souvenir . in。
第一行包含三个正整数T,N,M,相邻两数之间以一个空格分开，分别代表未来天数 T,纪念品数量N,小伟现在拥有的金币数量M。
接下来T行，每行包含N个正整数，相邻两数之间以一个空格分隔。第i行的N个正整数分别为Pi1,Pi2, …… ,Pin,其中Pi,j表示第i天第j种纪念品的价格。
【输出格式】
输出文件名为souvenir . out。
输出仅一行，包含一个正整数，表示小伟在超能力消失后最多能拥有的金币数量。
【输入输出样例1】
【 输入输出样例1说明】
最佳策略是：
第二天花光所有100枚金币买入5个纪念品1;
第三天卖出5个纪念品1,获得金币125枚；
第四天买入6个纪念品1,剩余5枚金币；
第六天必须卖出所有纪念品换回300枚金币，第四天剩余5枚金币，共305枚金币。
超能力消失后，小伟最多拥有305枚金币。
【输入输出样例2】
【输入输出样例2说明】
最佳策略是：
第一天花光所有金币买入10个纪念品1;
第二天卖出全部纪念品1得到150枚金币并买入8个纪念品2和1个纪念品3,剩 余1枚金币；
第三天必须卖出所有纪念品换回216枚金币，第二天剩余1枚金币，共217枚金币。 超能力消失后，小伟最多拥有217枚金币。
【数据规模与约定】
对于10%的数据，T=1。
对于30%的数据，T≤4,N≤4,M≤100,所有价格10≤Pij≤100。
另有15%的数据，T≤100,N=1。
另有15%的数据，T=2,N≤100。
对于100%的数据，T≤100,N≤100,M≤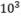
,所有价格1≤Pij≤10⁴,数 据保证任意时刻，小明手上的金币数不可能超过10⁴。
参考答案：对于本题，我们可以使用动态规划来解决。首先，我们定义一个二维数组dp[i][j]，其中dp[i][j]表示在第i天结束时，拥有j枚金币可以获得的最大金币数。然后，我们可以根据以下状态转移方程来更新dp数组：1. 如果在第i天结束时，小伟选择购买纪念品，则他可以选择在第i-1天结束时拥有j-P[i][k]枚金币，其中P[i][k]表示第i天第k种纪念品的价格。因此，dp[i][j] = max(dp[i][j], dp[i-1][j-P[i][k]] + P[i][k])。2. 如果在第i天结束时，小伟选择卖出纪念品，则他可以选择在第i-1天结束时拥有j+P[i][k]枚金币，其中P[i][k]表示第i天第k种纪念品的价格。因此，dp[i][j] = max(dp[i][j], dp[i-1][j+P[i][k]])。最后，我们只需要在最后一天结束时，遍历所有可能的金币数，找到最大的dp[T][j]即可。
4、加工零件
【问题描述】
凯凯的工厂正在有条不紊地生产一种神奇的零件，神奇的零件的生产过程自然也很 神奇。工厂里有n位工人，工人们从1～n编号。某些工人之间存在双向的零件传送 带。保证每两名工人之间最多只存在一条传送带。
如果x号工人想生产一个被加工到第L(L>1)阶段的零件，则所有 与 x 号 工 人 有传送带直接相连的工人，都需要生产一个被加工到第L- 1阶段的零件(但x号工 人自己无需生产第L - 1阶段的零件)。
如果x号工人想生产一个被加工到第1阶段的零件，则所有与x号工人有传送带直接 相连的工人，都需要为x号工人提供一个原材料。
轩 轩 是 1 号工人。现在给出q张工单，第i张工单表示编号为ai的工人想生产 一个第Li阶段的零件。轩轩想知道对于每张工单，他是否需要给别人提供原材料。他 知道聪明的你一定可以帮他计算出来!
【输入格式】
输入文件名为work.in。
第一行两个正整数n,m和q,分别表示工人的数目、传送带的数目和工单的数目。
接下来m行，每行两个正整数u和v,表示编号为u和v的工人之间存在 一条零 件传输带。保证u≠v。
接下来q行，每行两个正整数a和L,表示编号为a的工人想生产 一个第L阶段 的零件。
【输出格式】
输出文件名为work . out。
共q行，每行一个字符串“Yes”或者“No”。如果按照第i张工单生产，需要编号为 1的轩轩提供原材料，则在第i行输出“Yes”;否则在第i行输出“No”。注意输出不含 引号。
【输入输出样例 1】
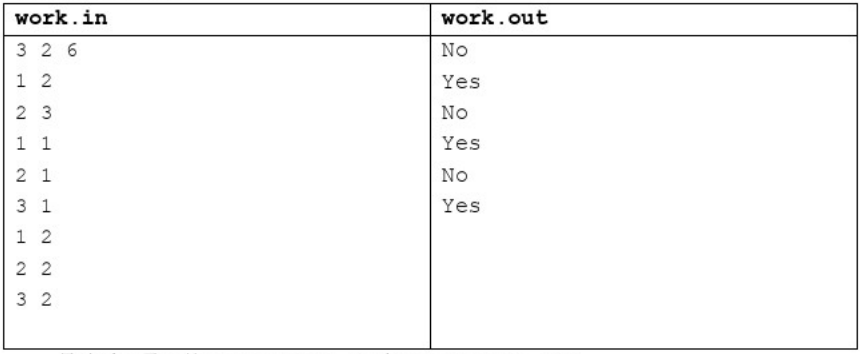
【输入输出样例1说明】
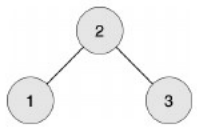
编号为1的工人想生产第1阶段的零件，需要编号为2的工人提供原材料。
编号为2的工人想生产第1阶段的零件，需要编号为1和3的工人提供原材料。
编号为3的工人想生产第1阶段的零件，需要编号为2的工人提供原材料。
编号为1的工人想生产第2阶段的零件，需要编号为2的工人生产第1阶段的零 件，需要编号为1和3的工人提供原材料。
编号为2的工人想生产第2阶段的零件，需要编号为1和3的工人生产第1阶段 的零件，他/她们都需要编号为2的工人提供原材料。
编号为3的工人想生产第2阶段的零件，需要编号为2的工人生产第1阶段的零件，需要编号为1和3的工人提供原材料。
【输入输出样例2】
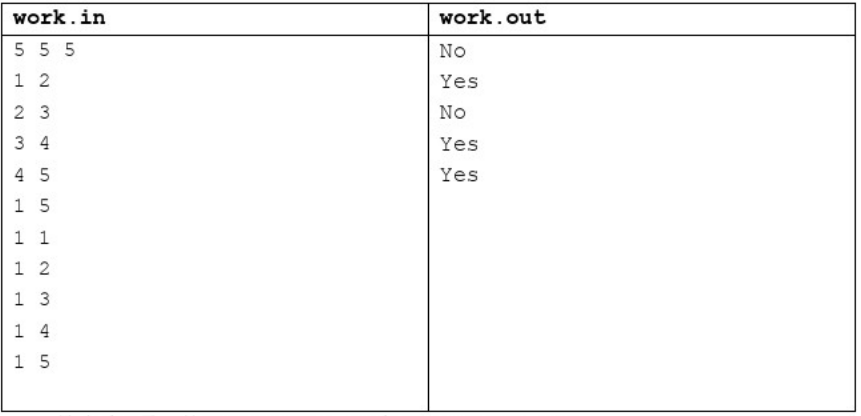
【输入输出样例2说明】
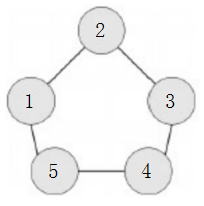
编号为1的工人想生产第1阶段的零件，需要编号为2和5的工人提供原材料。
编号为1的工人想生产第2阶段的零件，需要编号为2和5的工人生产第1阶段 的零件，需要编号为1,3,4 的工人提供原材料。
编号为1的工人想生产第3阶段的零件，需要编号为2和5的工人生产第2阶段的零件，需要编号为1,3,4的工人生产第1阶段的零件，需要编号为2,3,4,5 的工人提供 原材料。
编号为1的工人想生产第4阶段的零件，需要编号为2和5的工人生产第3阶段 的零件，需要编号为1,3,4的工人生产第2阶段的零件，需要编号为2,3,4,5 的工人生产 第1阶段的零件，需要全部工人提供原材料。
编号为1的工人想生产第5阶段的零件，需要编号为2和5的工人生产第4阶段 的零件，需要编号为1,3,4的工人生产第3阶段的零件，需要编号为2,3,4,5 的工人生产 第2阶段的零件，需要全部工人生产第1阶段的零件，需要全部工人提供原材料。
【数据规模与约定】
共20个测试点。
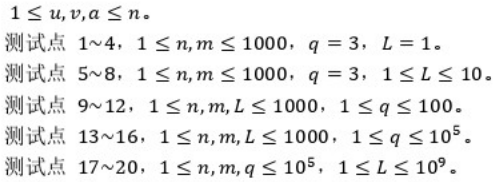
参考答案：对于每张工单，我们需要判断工人是否需要编号为1的轩轩提供原材料。
喵呜刷题：让学习像火箭一样快速，快来微信扫码，体验免费刷题服务，开启你的学习加速器！
