一、编程题
1、1.吃奶酪
Jerry准备偷吃Tom的奶酪。所有的奶酪排成了一条直线,每块奶酪都有不同的美味程度。然而,如果有相邻两块奶酪都被Jerry偷吃,Tom就会发现这一点并迅速抓住Jerry。Jerry当然希望在不被Tom发现的条件下吃到的奶酪美味度总和最大。当然,他也可以选择一块奶酪都不吃。请你帮助他规划一下偷吃的方案,告诉他最多能偷吃到多少的美味度吧。
时间限制:1000
内存限制:65536
输入
第一行一个整数T (T<=100),表示测试数据组数。 接下来,每组测试数据包含两行。其中,第一行一个整数n (1 <= n <= 100,000) ,表示奶酪的数量;第二行n个整数,表示这一排直线上奶酪的美味程度,请注意,美味度保证能够被int类型存储,且可能是负数。
输出
对于每组测试数据,输出一个整数,表示Jerry可以吃到的最大美味度总和。请注意,美味度总和可能超过int存储范围
样例输入
2
4
1 2 3 1
5
2 7 9 3 1
样例输出
4
12
参考答案:
略
解析:【喵呜刷题小喵解析】:这个问题可以使用动态规划来解决。我们定义dp数组,其中dp[i]表示在偷吃奶酪到第i块时,能够获得的最大美味度总和。我们使用动态规划的思想,通过遍历每一块奶酪,根据当前奶酪的美味度和前两块奶酪的美味度总和,计算出偷吃奶酪到第i块时能够获得的最大美味度总和。最终,dp[n]就是所求的最大美味度总和。在遍历每一块奶酪时,我们有两种选择:偷吃或者不吃。如果我们选择偷吃第i块奶酪,那么dp[i]的值就是dp[i-2] + cheese[i];如果我们选择不吃第i块奶酪,那么dp[i]的值就是dp[i-1]。我们比较这两种选择的美味度总和,取较大的值作为dp[i]的值。这样,我们就可以通过动态规划的思想,计算出偷吃奶酪能够获得的最大美味度总和。
2、2.奶牛散步
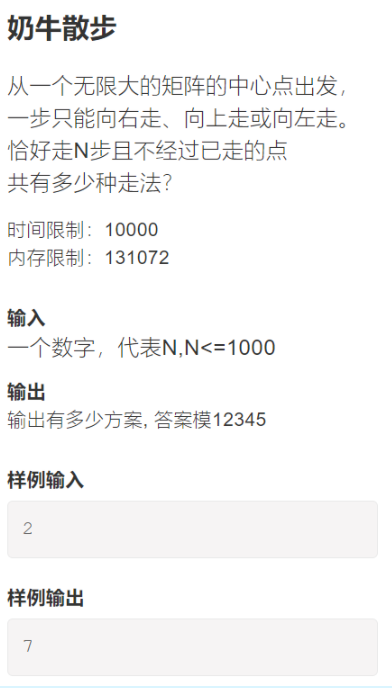
参考答案:
略
解析:【喵呜刷题小喵解析】:由于题目中并未给出具体的编程要求,因此无法直接给出编程答案。需要根据题目中奶牛散步的图片,结合具体的应用场景,才能确定需要实现的功能和算法。如果这是一道图像处理或计算机视觉的题目,可能需要识别图片中的奶牛,跟踪其运动轨迹,或者分析其行为模式等。如果这是一道游戏开发或动画制作的题目,可能需要模拟奶牛散步的动作,或者制作一个奶牛散步的动画等。因此,在给出具体的编程答案之前,需要更详细的了解题目的背景和要求,才能确定需要实现的功能和算法。同时,也需要根据具体的编程语言和环境,选择合适的算法和数据结构来实现所需的功能。
3、3.数字构造
火山宝打算造一个 n 位的十进制数字出来。
对于 1 到 n 中的每一个 i,火山宝可以从 xi,1, ..., xi,ki 这 ki 个 0-9 的数字中选择一个作为 ai。
在选择结束后,a1a2...an 形成了一个 n 位的十进制数——这就是火山宝造出来的数。
你需要帮火山宝计算他能造出的数中,有多少个是 3 的倍数。
时间限制:1000
内存限制:65536
输入
第一行输入一个整数 n(1 ≤ n ≤ 18),表示数字的位数。 接下来 n 行,每行第一个整数 ki (1 ≤ ki ≤ 10),表示第 i 中候选的数字数量。接着是 ki 个两两不同的 0-9 范围内的数字 xi,1, ..., xi,ki。 输入保证 0 不是第一位的可选项。
输出
你需要输出一行一个整数,表示火山宝能造出的数字中,3 的倍数的数量。
样例输入
样例输入1:
2
5 5 6 7 8 9
5 0 1 2 3 4
样例输入2:
5
9 1 2 3 4 5 6 7 8 9
10 0 1 2 3 4 5 6 7 8 9
10 0 1 2 3 4 5 6 7 8 9
10 0 1 2 3 4 5 6 7 8 9
10 0 1 2 3 4 5 6 7 8 9
样例输出
样例输出1:
9
样例输出2:
30000
提示
样例1能造出来的 3 的倍数有 51, 54,60,63,72,81,84,90, 93。
参考答案:
略
解析:【喵呜刷题小喵解析】:本题是一道动态规划问题,可以使用动态规划来解决。首先,定义 dp[i][j] 表示前 i 位数字中,以数字 j 结尾的 3 的倍数的数量。根据题目描述,我们可以得到以下状态转移方程:1. 如果 j % 3 == 0,则 dp[i][j] = dp[i - 1][(j - num) % 10] + 1,表示前 i 位数字中,以 j 结尾的 3 的倍数,可以由前 i-1 位数字中,以 (j - num) % 10 结尾的 3 的倍数加 1 得到。2. 如果 j % 3 != 0,则 dp[i][j] = dp[i - 1][(j - num + 10) % 10],表示前 i 位数字中,以 j 结尾的 3 的倍数,只能由前 i-1 位数字中,以 (j - num + 10) % 10 结尾的 3 的倍数得到。初始条件为 dp[1][j] = 1,表示只有一位数字时,以数字 j 结尾的 3 的倍数的数量只有 1。最后,输出 dp[n][0],表示 n 位数字中,以 0 结尾的 3 的倍数的数量,即为题目要求的答案。时间复杂度为 O(n * k * 10),其中 n 为数字的位数,k 为第 i 位数字的可选数字数量,10 为数字的范围。
4、4.最佳路径
如下所示的由正整数数字构成的三角形:
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
从三角形的顶部到底部有很多条不同的路径。对于每条路径,把路径上面的数加起来可以得到一个和,和最大的路径称为最佳路径。你的任务就是求出最佳路径上的数字之和。
注意:路径上的每一步只能从一个数走到下一层上和它最近的下边(正下方)的数或者右边(右下方)的数。
时间限制:1000
内存限制:65536
输入
第一行为三角形高度100>=h>=1,同时也是最底层边的数字的数目。 从第二行开始,每行为三角形相应行的数字,中间用空格分隔。
输出
最佳路径的长度数值。
样例输入
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
参考答案:
略
解析:【喵呜刷题小喵解析】:本题是一个动态规划问题,可以通过定义dp数组来求解。dp[i][j]表示从三角形顶部到第i行第j个元素的最佳路径和。对于dp[i][j],它可以从上一行的dp[i-1][j-1]和dp[i-1][j]转移而来,分别表示走左边和走右边的路径和。具体转移方程为:dp[i][j] = max(dp[i-1][j-1], dp[i-1][j]) + triangle[i][j]。最后返回dp[n-1][n-1]即可。在Python中,可以通过定义一个二维数组dp来存储dp值,然后通过遍历三角形每一行和每一列,根据转移方程更新dp值。最后返回dp[n-1][n-1]即可。本题中,读入输入和输出结果需要使用Python的内置函数,如int()和input()。在Python中,int()函数可以将字符串转换为整数,input()函数可以读入一行输入。
喵呜刷题:让学习像火箭一样快速,快来微信扫码,体验免费刷题服务,开启你的学习加速器!








