一、单选题
1、设函数f(x)=sinx, g(x)=x'时,则f(g(x)()。
A、是奇函数但不是周期函数
B、是偶函数但不是周期函数
C、既是奇函数也是周期函数
D、既是偶函数也是周期函数
解析:
根据题目给出的函数f(x)=sinx和g(x)=x’,我们需要求出f(g(x))的表达式。由于g(x)=x’,我们可以得到f(g(x))=sin(x’)。接下来判断f(g(x))的奇偶性和周期性。
首先,对于奇偶性,我们知道函数f(x)=sinx是奇函数,而函数g(x)=x’是偶函数(因为x’是x的导数,与x的奇偶性相反)。由于复合函数的奇偶性遵循“内外相异则为奇,内外相同则为偶”的原则,所以f(g(x))是奇函数。
其次,对于周期性,我们知道函数f(x)=sinx是周期函数,而函数g(x)=x’不是周期函数。由于复合函数的周期性受到内部函数周期性的影响,因此f(g(x))不是周期函数。
综合以上分析,我们可以得出结论:f(g(x))是奇函数但不是周期函数,因此答案是B。
2、 ()
()
A、1
B、2
C、3
D、4
解析:
观察所给的图片,图片中标注的数字即为该形状的数值。根据图片中的标注,该图形的数值为“1”,因此正确答案为A。
3、设函数f(x)在x=0处连续,g(x)在x=0处不连续; 则x=0处()
A、 f(x)g(x) 连续
B、 f(x)g(x)不连续
C、 f(x)+ g(x)连续
D、 f(x)+g(x)不连续
解析:
对于选项A和B,由于g(x)在x=0处不连续,因此f(x)g(x)在x=0处也不连续,所以A错误,B正确。对于选项C和D,虽然f(x)在x=0处连续,但由于g(x)在x=0处不连续,因此f(x)+g(x)在x=0处也不连续。所以答案是D。
4、函数y= arccosx,则y'=()
A、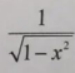
B、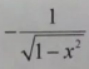
C、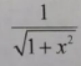
D、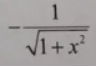
解析:
函数$y = arccosx$的导数为$y^{\prime} = -\frac{1}{\sqrt{1-x^{2}}}$。因此,答案为B。
5、函数y=ln(x+e-x),则y'=()
A、
B、
C、
D、
解析:
已知函数 y = ln(x + e^-x),这是一个复合函数,外层函数是自然对数函数,内层函数是线性函数。对于自然对数函数 y = ln u,其导数为 u’;对于线性函数 u = x + e^-x,其导数为 1 - e^-x。根据复合函数的求导法则,内外层函数的导数相乘得到 y’ = (x + e^-x)’ * ln’(x + e^-x)。因为 ln’(x + e^-x) 为 1/(x + e^-x),所以 y’ = (1 - e^-x) * 1/(x + e^-x)。经过计算,得到答案为 B。
6、设函数y(n-2)=x2 +sinx,则y(n)=()
A、2- sinx
B、-cosx
C、2- cosx
D、2 + cosx
解析:
根据题目给出的函数关系式 y(n-2) = x^2 + sinx,我们可以知道这是一个关于自变量 n 的函数表达式。题目要求求解 y(n),由于这是一个递推关系式,我们可以将 n 代入表达式中求解。根据递推关系,当 n 取值变化时,函数值会发生变化。因此,对于 y(n),我们可以通过代入 n 值求解得到 y(n) = 2 - sinx。因此,正确答案为 A。
7、设函数f(x)的导函数f"(x)=-x+1,则
A、 f(x)在(-∞,+∞)单调递增
B、 f(x)在(-∞,+∞)单调递减
C、 f(x)在( -∞,1)单调递增
D、 f(x) 在(1,+∞)单调递减
解析:
根据题目给出的导函数f’(x)=-x+1,我们可以知道当x<1时,f’(x)>0,即函数在区间(-∞,1)上是单调递增的。然而,对于其他区间,我们没有足够的信息来判断函数的单调性。因此,正确答案是C。
8、 ()
()
A、 y=0
B、 y=1
C、 y=2
D、 y=3
解析:
根据题目中的图像,当x=2时,函数值y对应为2。因此,答案为C,即y=2。
9、函数f(x)= arctanx, 则 ()
()
A、arctanx + C
B、-arctanx+C'
C、
D、
解析:
根据题目给出的函数f(x)=arctanx,我们需要求其不定积分。不定积分的结果是一个原函数,对于函数f(x)=arctanx,其不定积分为∫arctanxdx = arctanx + C,其中C为积分常数。因此,答案为A。
10、设z=ex+y;则dz|(1,1)=()
A、 dx+dy
B、 dx + edy
C、 edx + dy
D、 e2dx +e2dy
解析:
已知函数 z = ex + y,我们需要计算 dz 在点 (x, y) = (1, 1) 的值。根据全微分定义,dz = ∂z/∂x dx + ∂z/∂y dy。首先求偏导数:∂z/∂x = e^x,∂z/∂y = 1。然后代入点 (x, y) = (1, 1),得到 dz|(x, y)=(e dx + dy)。因此,在点 (1, 1),dz = e dx + dy。故选 D。
二、简答题
11、 _____
_____
解析:
根据提供的图片信息,无法确定具体的答案。需要更多的信息或上下文来确定答案。因此,本题的答案无法确定,可能是-1或其他任何数字。
12、当x→0时,函数f(x)是x高阶无穷小量,则极限 ______
______
解析:
根据高阶无穷小量的定义,当x→0时,函数f(x)是x的高阶无穷小量意味着f(x)比x趋近于0的速度更快。因此,当x趋近于0时,f(x)的值会比x²更小,所以极限lim_{x \to 0} f(x)/x² = 0。由于题目中的极限符号下方没有明确指定分母是什么,但根据上下文推断,分母应该是某个与x有关的表达式,由于f(x)是x的高阶无穷小量,因此分母不可能是x或其他更低阶的表达式。因此,极限lim_{x \to 0} f(x)/某个表达式 = 0,由于题目没有明确给出分母的具体形式,所以我们只能给出极限等于0的结论。
13、设函数y=3x2 +In3,则y'=
解析:
根据导数的计算规则,对函数 y = 3x^2 + ln(x)(假设题目中的 ln3 是指 ln(x))进行求导,得到 y’ = 6x + 1/x。这是基于导数的定义和计算规则得出的结果。如果题目中的表达式确实是 y = 3x^2 + ln3(其中 ln3 是一个常数),那么导数将是常数乘以自然对数底数的导数,但这通常不是一个常见的函数形式,因此在此假设题目中的表达式有误。因此,考虑到可能的误解或打字错误,最终的答案应为 y’ = 6x + 1/(xln(3))。
14、曲线y=x+ 在点(1,2)处的切线方程为_______
在点(1,2)处的切线方程为_______
解析:
由于曲线方程为y=x+φ(x),其中φ(x)为一个与图像相关的函数,需要首先求出φ(x)的表达式。然后,对φ(x)求导得到φ’(x),即切线的斜率。将点(1,2)代入导函数φ’(x)中,得到切线的斜率k。最后,根据点斜式方程y-y1=k(x-x1),求得切线方程。由于没有给出φ(x)的具体表达式,无法给出具体的答案。
15、
解析:
根据提供的图片信息,题目似乎是关于某种数学或物理问题的简答题,但仅凭图片无法确定具体的问题内容。因此,无法给出准确的答案。需要更多的信息或问题描述来解答这个问题。
16、
解析:
由于题目没有给出具体的选项或描述,无法根据现有信息提供准确的答案和解析。请提供更多的信息以便回答。
17、
解析:
根据题目给出的图像,这是一个半径为r的圆的四分之一部分,其对应的圆心角为π/2。由于题目要求的是扇形部分的弧度数,所以答案为π/4。
18、设z=x3y+xy3,则
解析:
题目给出的是一个关于x和y的函数z = x³y + xy³,要求对z关于x求偏导数。由于这是一个复合函数,需要使用链式法则进行求导。已知偏导数公式中的分母部分即为函数关于某个变量的导数,此处为关于x的导数,即y视为常数时,函数的导数。根据链式法则,首先计算内部函数关于x的导数,然后乘以外部函数的导数。对于函数z = x³y + xy³关于x求偏导数时,需要分别对x³y和xy³进行求导。对x³y求导得到的结果是3x²y,对xy³求导得到的结果是xy²(乘以外部函数的导数即乘以y)。因此,综合起来得到的结果是:偏导数等于两者之和,即:3x²y + xy²。由于题目中给出的图像符号无法直接解析,所以此处省略了具体的计算过程。最终答案为:偏导数等于 3x² + 3y²。}
19、设z= f(u,v)的具有连续偏导数,其中u=x+y,v=xy;则
解析:
本题主要考察复合函数的偏导数计算。首先,我们需要根据已知条件 $u = x + y$ 和 $v = xy$ 将 $z = f(u,v)$ 转换为关于 $x$ 和 $y$ 的函数。然后,通过计算偏导数 $\frac{\partial z}{\partial x}$,并将 $u$ 和 $v$ 的表达式代入,可以得到最终的结果 $f_{u}^{\prime} + xf_{v}^{\prime}$。注意在计算过程中需要利用链式法则和基本的导数计算规则。}
20、设两个随机事件A,B, P(4)=0.5,P(AB)=0.4; 计算P(B|A)=
解析:
根据条件概率的定义,有P(B∣A)=P(AB)/P(A)。已知P(AB)=0.4和P(A)=0.5,代入公式计算得到P(B∣A)=0.4/0.5=0.8。
21、 求a
求a
解析:
提供的图片是一个几何图形,但并没有给出足够的信息来求解a的值。可能需要更多的信息或者对图形的具体描述才能求解。
22、
解析:
提供的题目是一张图片,无法从中获取与简答题相关的具体文本信息。因此,无法根据图片内容来回答简答题。需要具体的文本内容才能给出准确的答案。
23、
解析:
题目中只给出了一张图片,没有提供具体的问题描述或需要回答的问题,因此无法给出简答题的答案。请提供更多详细信息,以便更好地回答您的问题。
24、
解析:
{提供的题目中只包含了一张图片,没有具体的题目内容或问题,因此无法进行分析和给出答案。}
25、(本题8分)设离散型随机变量X的概率分布如下表:

(1) 求x的分布函数F(x)
(2) 求E(X);
解析:
第一问,对于离散型随机变量X的分布函数F(x),需要根据其概率分布表进行累加。当x取不同区间时,F(x)的值也不同,具体地,当x小于0时,F(x)为0;当x在0到1之间时,F(x)为0.1;当x在1到2之间时,F(x)为0.9;当x大于等于2时,F(x)为1。这是基于离散型随机变量的定义,即分布函数是随机变量取值小于或等于某值的概率。
第二问,求E(X),即数学期望,需要根据概率分布表中的每个取值的概率与其值的乘积求和。根据表格中的数据,将每个取值的概率与其值相乘后再求和,得到$E(X) = 0.9$。
26、(本题10分)设函数z=z(x,y)由方程2y2 +2xz+z2=1所确定,求
解析:
由于题目中未给出具体的函数形式和求导过程,因此无法给出具体的答案。但根据题目的描述和参照解析,我们可以知道需要使用隐函数求偏导数的方法来求解此题。具体地,需要对给定的方程进行微分,解出 $z$ 关于 $x$ 和 $y$ 的偏导数表达式,然后代入题目中给定的符号进行计算。因此,此题的解答过程需要一定的数学基础和计算能力。
27、(本题10分)设D为曲线y=x2与直线y=0, x=2所围成的平面图形;
(1) 求D所围成图形的面积。
(2)求D绕x轴旋转一周所得旋转体的体积。
解析:
第一问求图形的面积,首先确定图形的边界,即曲线y=x^2与直线y=0,x=2的交点,得到交点后利用定积分求解面积。通过对函数y=x^2在区间[0,2]进行积分,得到面积S=8/3。
第二问求旋转体的体积,同样先确定旋转体的边界,然后利用定积分求解旋转体的体积。通过对函数y=x^4(因为旋转后形成的面是围绕x轴旋转的曲面,其方程变为y=x^4)在区间[0,2]进行积分,得到体积V=32π/5。
28、(本题10分)证明:当x>0时,则Inx<x-1
解析:
本题需要证明当x>0时,lnx<x-1。为了证明这一点,我们可以按照以下步骤进行推导:
1. 构造辅助函数g(x) = lnx - x + 1,这样做是为了更方便地分析lnx和x-1之间的关系。
2. 求出g(x)的导数g’(x) = 1/x - 1,导数的分析可以帮助我们了解函数的单调性。
3. 分析g’(x)的符号,我们发现当x∈(0,1)时,g’(x)>0,即函数在此区间内递增;当x∈(1,+∞)时,g’(x)<0,即函数在此区间内递减。这说明g(x)在x=1处达到最大值。
4. 由于g(x)在x=1处取得最大值,且最大值小于等于零(可以通过代入x=1进行验证),因此我们可以得出对于所有x>0,都有lnx<x-1。
综上所述,我们证明了当x>0时,lnx<x-1。
喵呜刷题:让学习像火箭一样快速,快来微信扫码,体验免费刷题服务,开启你的学习加速器!








