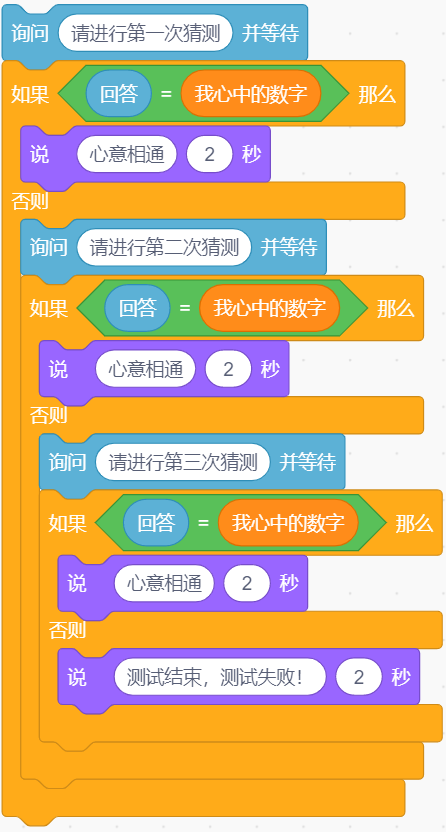
小猫为了测试双胞胎之间是否能够真的做到心意相通,设计了一个程序,如下图所示:一人心中想着一个十以内的数,另一人猜测,共有3次猜测机会。下列哪个选项可以优化这个程序?( )
刷题刷出新高度,偷偷领先!偷偷领先!偷偷领先! 关注我们,悄悄成为最优秀的自己!
小猫为了测试双胞胎之间是否能够真的做到心意相通,设计了一个程序,如下图所示:一人心中想着一个十以内的数,另一人猜测,共有3次猜测机会。下列哪个选项可以优化这个程序?( )

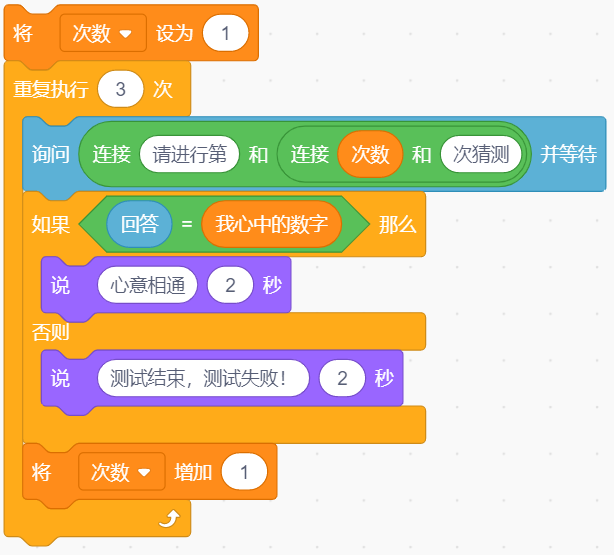
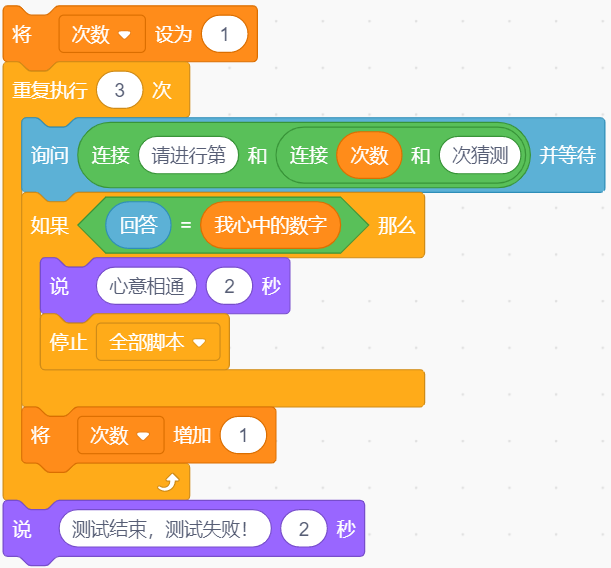
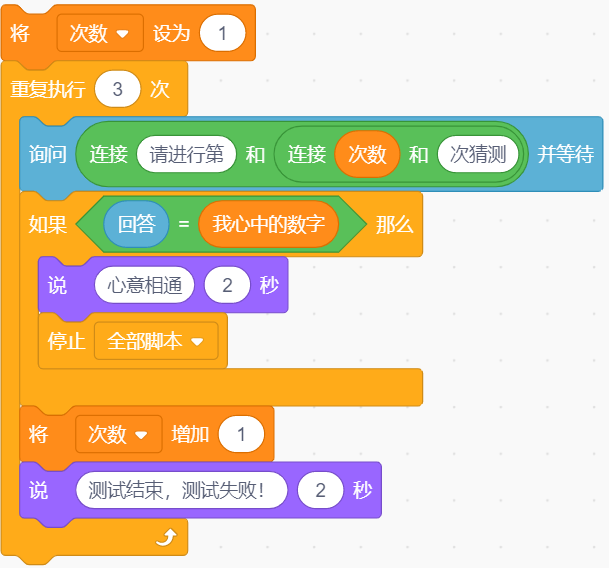

本文链接:小猫为了测试双胞胎之间是否能够真的做到心意相通,设计了一个程序,如下图所示:一人心中想着一个十以内的
版权声明:本站点所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明文章出处。让学习像火箭一样快速,微信扫码,获取考试解析、体验刷题服务,开启你的学习加速器!
