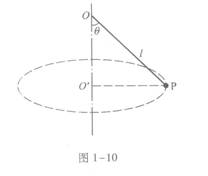
1.56 m,已知小球在水平面内做以O'为圆心的匀速圆周运动,悬线与竖直方向的夹角θ=45°.求
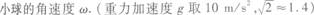
刷题刷出新高度,偷偷领先!偷偷领先!偷偷领先! 关注我们,悄悄成为最优秀的自己!

{本题是匀速圆周运动的试题,主要考察牛顿第二定律和向心力知识点。首先,根据受力分析得到小球受细线的拉力和重力作用,且合力提供向心力。然后,根据三角函数关系得到细线拉力、向心加速度与重力之间的关系。接着,利用牛顿第二定律求出向心加速度和角速度。最后,根据周期与角速度的关系求出周期。具体过程如下:
综上所述,细线拉力为mg×tanθ,小球运动的角速度为ω=√(gtanθ/lsinθ),周期为T=2π√(lcosθ/g)。}
本文链接:如图1-10所示,细线的上端固定于O点,下端系一个小球P,线长l= 1.56 m,已知小球在水平面内
版权声明:本站点所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明文章出处。让学习像火箭一样快速,微信扫码,获取考试解析、体验刷题服务,开启你的学习加速器!
