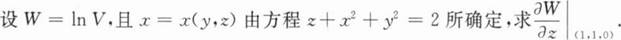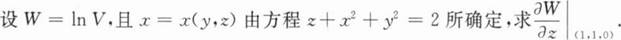基于给定的图像信息，解答以下问题： (1) 求出由处的切平面与三坐标面围成的四面体的体积表达式V，并求出其最小值。 (2) 请根据图像信息进行分析。

(1)首先，根据题目描述，我们知道四面体是由切平面与三坐标面围成的。假设切平面上有一点M的坐标为$(x_{0}, y_{0}, z_{0})$，由于切平面与坐标面相交，我们可以得到四面体的三个边分别与x轴、y轴、z轴有关。因此，我们可以通过计算四面体的底面积和高来得到体积的表达式。根据几何知识，四面体的体积可以表示为$V = \frac{1}{3} \times \text{底面积} \times \text{高}$。其中，底面积可以通过切平面与坐标面的交点来计算，高则是点M到原点的距离。因此，我们可以得到四面体体积的表达式为$V = \frac{1}{3} \times \frac{x_{0}^{2}}{a^{2}} \times \frac{y_{0}^{2}}{b^{2}} \times z_{0}$。当点M位于原点时，即$x_{0}=y_{0}=z_{0}=0$时，四面体的体积达到最小值，即$V_{\min} = 0$。

(2)由于题目没有给出关于第二问的具体信息，因此无法给出详细的解答。