刷题刷出新高度,偷偷领先!偷偷领先!偷偷领先! 关注我们,悄悄成为最优秀的自己!
二次型f(x1, x2, x3) = (x1 - x2)2 + (x2 - x3)2 + (x3 - x1)2的标准形式为?

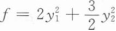

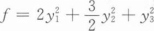
答案:
解析:
对于给定的二次型$f(x_{1},x_{2},x_{3})=(x_{1}-x_{2})^{2}+(x_{2}-x_{3})^{2}+(x_{3}-x_{1})^{2}$,我们可以通过配方的方法将其转化为标准型。
首先,我们可以将每一项平方展开,得到$f(x_{1},x_{2},x_{3})=x_{1}^{2}-2x_{1}x_{2}+x_{2}^{2}+x_{2}^{2}-2x_{2}x_{3}+x_{3}^{2}+x_{3}^{2}-2x_{3}x_{1}+x_{1}^{2}$。
接着,我们可以将含有$x_1, x_2, x_3$的项进行组合,得到$f(x_{1},x_{2},x_{3})=3(x_{1}^{2}+x_{2}^{2}+x_{3}^{2})-6(x_1 x_2 + x_2 x_3 + x_3 x_1)$。
然后,我们可以完成配方,将上式写为$f(x_{1},x_{2},x_{3})=3[(x_{1}-x_{2})^{2}+(x_{2}-x_{3})^{2}+(x_{3}-x_{1})^{2}]$。
最后,我们可以看到,这个二次型可以写为标准型的形式,即$f(x_{1},x_{2},x_{3})=\lambda_1 y_1^2 + \lambda_2 y_2^2 + \lambda_3 y_3^2$,其中$\lambda_1 = \lambda_2 = \lambda_3 = 3$。因此,答案是B。
本文链接:二次型f(x1, x2, x3) = (x1 - x2)2 + (x2 - x3)2 + (x3 -
版权声明:本站点所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明文章出处。让学习像火箭一样快速,微信扫码,获取考试解析、体验刷题服务,开启你的学习加速器!



