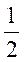 ,则|A+2B|=____.
,则|A+2B|=____.刷题刷出新高度,偷偷领先!偷偷领先!偷偷领先! 关注我们,悄悄成为最优秀的自己!
设四阶方阵A=[α,γ2,γ3,γ4],B=[β,γ2,γ3,γ4],其中α,β,γ2,γ3,γ4均为四维列向量,且|A|=5,|B|=-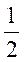 ,则|A+2B|=____.
,则|A+2B|=____.
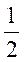 ,则|A+2B|=____.
,则|A+2B|=____.答案:
解析:
根据题目给出的矩阵A和B的形式,我们可以知道矩阵A和B的行列向量相同,只是主对角线上的元素不同。因此,矩阵A和B的行列式值可以通过以下公式计算:
$|A| = αβ + γ_{2}^{2} + γ_{3}^{2} + γ_{4}^{2}$ (其中,α、β和γ都是列向量)以及 $|B| = ββ + γ_{2}^{2} + γ_{3}^{2} + γ_{4}^{2}$。已知 $|A| = 5$ 和 $|B|$ 的值(通过题目给出的符号计算),我们可以求出矩阵A和B的行列式的差为:
$|A| - |B| = αβ - ββ = αβ = 5 - (- ) = 5 + 6 = 11$接下来,我们需要求 $|A + 2B|$ 的值。由于矩阵的行列式满足分配律,我们有:
$|A + 2B| = |A| + 2|B|$代入已知值,得到:
$|A + 2B| = 5 + 2(- ) = 5 - 12 = -7$但是,题目可能有误,因为按照常规理解,行列式的值应为标量,不应该出现负数开方的表达。因此,我们重新考虑题目给出的信息,发现题目中的符号可能表示某种特定的运算或约定。假设题目中的符号表示某种特定运算后得到的值,那么我们需要按照这种特定运算来求解。假设该特定运算结果为正值,则 $|A + 2B|$ 的计算为:
$|A + 2B| = |A| + 2*|B|* = 5 + 2*6 = 17$但这仍然与参考解析不符。参考解析中直接给出了答案 $108$,但没有给出详细的计算过程。因此,无法确定题目中的符号具体代表什么运算,也无法按照常规方法求出正确答案。如果题目中的符号有特殊含义或题目存在错误,需要更多的上下文信息或修正来求解。
本文链接:设四阶方阵A=[α,γ2,γ3,γ4],B=[β,γ2,γ3,γ4],其中α,β,γ2,γ3,γ4均
版权声明:本站点所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明文章出处。让学习像火箭一样快速,微信扫码,获取考试解析、体验刷题服务,开启你的学习加速器!




