正交矩阵．

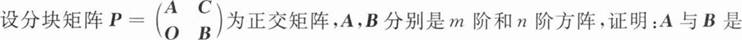
证明一个矩阵是正交矩阵的关键在于证明该矩阵的逆矩阵等于其转置矩阵。可以通过以下步骤进行证明：
1. 首先，计算矩阵的逆矩阵。如果矩阵A是可逆的，那么存在另一个矩阵B，使得AB=BA=单位矩阵。B就是A的逆矩阵。
2. 然后，计算矩阵的转置矩阵。对于任意一个mn矩阵A，其转置矩阵A’是一个nm矩阵，满足A’的元素是A的元素按照行列互换得到的。
3. 最后，验证逆矩阵是否等于转置矩阵。如果两者相等，则矩阵A是正交矩阵。

具体计算过程中，需要利用矩阵运算的基本性质，如矩阵乘法的结合律、分配律等。同时，需要注意保持计算的准确性和精度，避免出现计算错误。