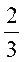 ,则b=______,ε=______.
,则b=______,ε=______.刷题刷出新高度,偷偷领先!偷偷领先!偷偷领先! 关注我们,悄悄成为最优秀的自己!
简答题
设x在区间[-1,b]上服从均匀分布,由切比雪夫不等式,有P{|X-1|<ε)≥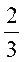 ,则b=______,ε=______.
,则b=______,ε=______.
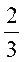 ,则b=______,ε=______.
,则b=______,ε=______.使用微信搜索喵呜刷题,轻松应对考试!
答案:
解析:
根据题目给出的信息,我们知道$X$在区间$\lbrack - 1,b\rbrack$上服从均匀分布。由切比雪夫不等式的性质,我们有$P(|X - 1| < \varepsilon) \geq 1 - \frac{1}{k^{2}}$,其中$k$是区间长度与总长度的比值。在这个问题中,区间长度是$b - (-1) = b + 1$,总长度是区间$\lbrack - 1,b\rbrack$的长度,即$b - (-1) = b + 1$。因此,我们可以得到$k = \frac{b + 1}{b + 2}$。代入切比雪夫不等式中,我们得到不等式$\frac{b + 2 - \varepsilon}{b + 2} \geq \frac{3}{4}$。解这个不等式,我们可以得到$\varepsilon = 2$和$b = 3$。
创作类型:
原创
本文链接:设x在区间[-1,b]上服从均匀分布,由切比雪夫不等式,有P{|X-1|<ε)≥,则b=______
版权声明:本站点所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明文章出处。让学习像火箭一样快速,微信扫码,获取考试解析、体验刷题服务,开启你的学习加速器!




