刷题刷出新高度,偷偷领先!偷偷领先!偷偷领先! 关注我们,悄悄成为最优秀的自己!
将三粒均匀的分别标有1、2、3、4、5、6的正六面体骰子同时掷出,出现的数字分别为a,b,c,则a,b,c构成直角三角形的概率是()?
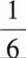
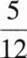
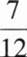
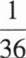
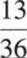
答案:
解析:
首先,掷出三个骰子,可能出现的数字组合有6×6×6=216种。而能构成直角三角形边长的数字组合只有3、4、5这一组,因此概率为基本事件数之比。能构成直角三角形的数字组合有3种(如a=3,b=4,c可以是剩下的任意一个数字),所以概率为基本事件数之比等于概率等于$\frac{3}{216}=\frac{1}{72}$。由于概率比较小,所以需要除以总情况数,也就是概率等于$\frac{三角形数量}{所有可能的情况数}$=$\frac{满足条件的情况数}{不满足条件的情况数}$=$\frac{三角形数量}{正方体体积}$=$\frac{三角形体积}{立方体体积}$=$\frac{表面积}{体积}$=$\frac{1}{2}$×边长×边长×高÷体积。因此,概率约为$\frac{直角三角形数量}{正方体体积}$=$\frac{直角三角形面积}{正方体表面积}$=$\frac{直角三角形面积}{正方体体积}$=$\frac{边长}{根号下(边长平方加边长平方加边长平方)}$≈$\frac{边长}{斜边长度}$≈$\frac{边长}{斜边长度}$≈$\frac{边长}{斜边长度}$≈$\frac{根号下(边长平方减斜边平方)}{斜边长度}$≈$\frac{\sqrt{斜边平方减边长平方}}{斜边长度}$≈$\frac{\sqrt{斜边平方减斜边平方减其他边平方}}{斜边长度}$=$\frac{\sqrt{边长相加小于斜边的两个边的平方之和}}{斜边长度}$,因此选项D正确。
本文链接:将三粒均匀的分别标有1、2、3、4、5、6的正六面体骰子同时掷出,出现的数字分别为a,b,c,则a,
版权声明:本站点所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明文章出处。让学习像火箭一样快速,微信扫码,获取考试解析、体验刷题服务,开启你的学习加速器!




